Papers
2024
-
Dynamic Data Layout Optimization with Worst-case GuaranteesKexin Rong, Paul Liu, Sarah Ashok Sonje, Moses Charikar
[pdf] [poster] [slides]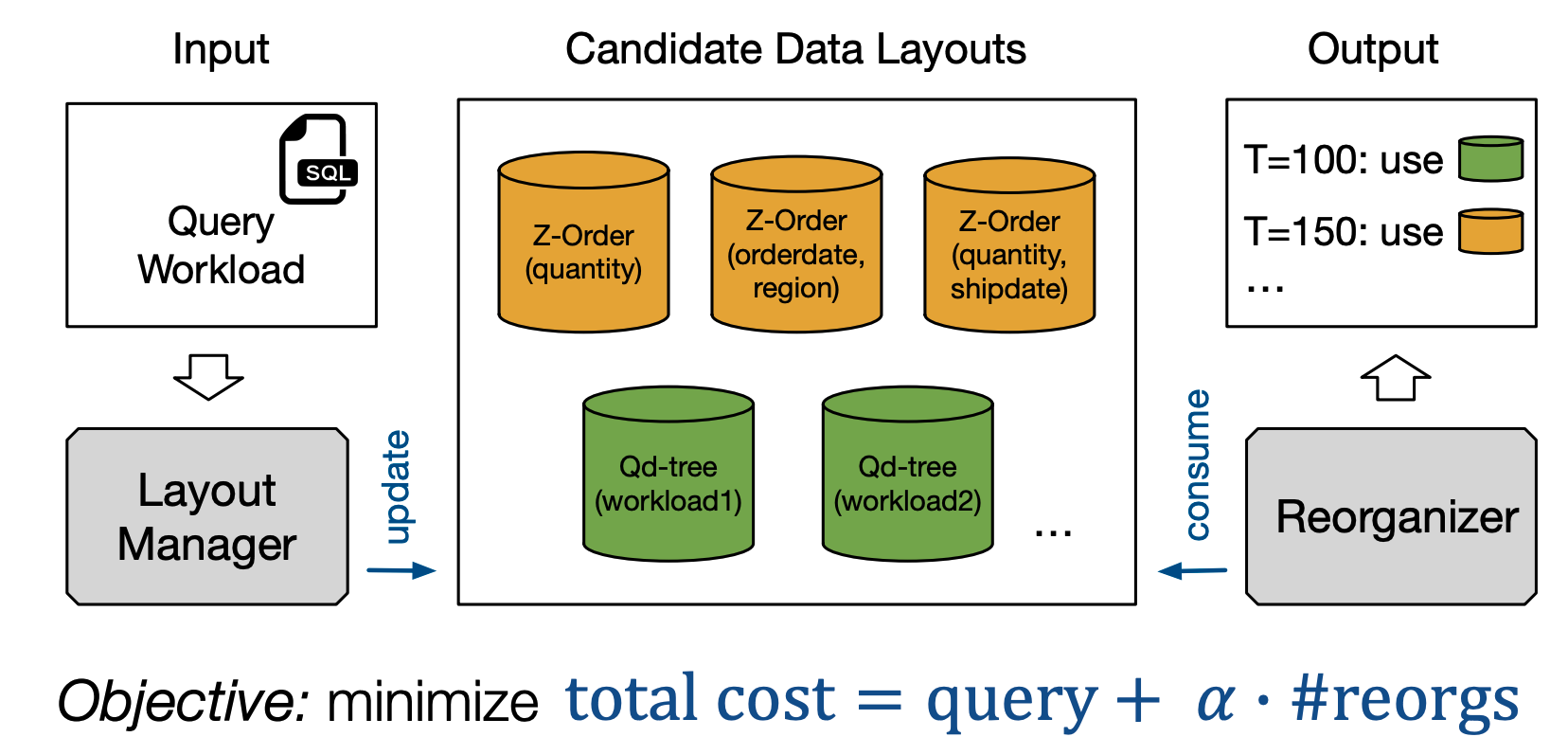
Many data analytics systems store and process large datasets in partitions containing millions of rows. By mapping rows to partitions in an optimized way, it is possible to improve query performance by skipping over large numbers of irrelevant partitions during query processing. This mapping is referred to as a data layout. Recent works have shown that customizing the data layout to the anticipated query workload greatly improves query performance, but the performance benefits may disappear if the workload changes. In this paper, we provide improved algorithms with theoretical guarantees for the layout optimization problem.
2023
-
Faster Submodular Maximization for Several Classes of MatroidsMonika Henzinger, Paul Liu, Jan Vondrak, Da Wei Zheng
[pdf]In this work, we develop algorithms for monotone submodular maximization constrained by graphic, transversal matroids, or laminar matroids in time near-linear in the size of their representation. Our algorithms achieve an optimal approximation of 1−1/e−ϵ and both generalize and accelerate the results of Ene and Nguyen [ICALP '19]. In fact, the running time of our algorithm cannot be improved within the fast continuous greedy framework of Badanidiyuru and Vondrák [SODA '14].
2022
-
MonoTrack: Shuttle trajectory reconstruction from monocular badminton videoPaul Liu and Jui-Hsien Wang
[pdf]
Trajectory estimation is a fundamental component of racket sport analytics, as the trajectory contains information not only about the winning and losing of each point, but also how it was won or lost. In sports such as badminton, players benefit from knowing the full 3D trajectory, as the height of shuttlecock or ball provides valuable tactical information. Unfortunately, 3D reconstruction is a notoriously hard problem, and standard trajectory estimators can only track 2D pixel coordinates. In this work, we present the first complete end-to-end system for the extraction and segmentation of 3D shuttle trajectories from monocular badminton videos. Our system integrates badminton domain knowledge such as court dimension, shot placement, physical laws of motion, along with vision-based features such as player poses and shuttle tracking. We find that significant engineering efforts and model improvements are needed to make the overall system robust, and as a by-product of our work, improve state-of-the-art results on court recognition, 2D trajectory estimation, and hit recognition.
-
Streaming Submodular Maximization under Matroid ConstraintsMoran Feldman, Paul Liu, Ashkan Norouzi-Fard, Ola Svensson, Jan Vondrák, and Rico Zenklusen
[pdf]Recent progress in (semi-)streaming algorithms for monotone submodular function maximization has led to tight results for a simple cardinality constraint. However, current techniques fail to give a similar understanding for natural generalizations, including matroid constraints. Our paper improves on the previously best approximation guarantees of $1/4$ and $1/2$ for single-pass and multi-pass streaming algorithms, respectively. In fact, our multi-pass streaming algorithm is tight in that any algorithm with a better guarantee than $1/2$ must make several passes through the stream and any algorithm that beats our guarantee of $1-1/e$ must make linearly many passes (as well as an exponential number of value oracle queries).
2021
-
Cardinality constrained submodular maximization for random streamsPaul Liu, Aviad Rubinstein, Jan Vondrák, Junyao Zhao
[pdf] [code] [poster] [slides]
We consider the problem of maximizing submodular functions in single-pass streaming and secretaries-with-shortlists models, both with random arrival order. For cardinality constrained monotone functions, Agrawal, Shadravan, and Stein gave a single-pass $(1-1/e-\varepsilon)$-approximation algorithm using only linear memory, but their exponential dependence on $\varepsilon$ makes it impractical even for $\varepsilon=0.1$. We simplify both the algorithm and the analysis, obtaining an exponential improvement in the $\varepsilon$-dependence (in particular, $O(k/\varepsilon)$ memory). Extending these techniques, we also give a simple $(1/e-\varepsilon)$-approximation for non-monotone functions in $O(k/\varepsilon)$ memory. For the monotone case, we also give a corresponding unconditional hardness barrier of $1-1/e+\varepsilon$ for single-pass algorithms in randomly ordered streams, even assuming unlimited computation.
Finally, we show that the algorithms are simple to implement and work well on real world datasets.
-
Improving Query Categorization with Categorical Graph Neural NetworksTianchuan Du, Keng-Hao Chang, Paul Liu, Ruofei Zhang
[pdf]
We propose a class of graph-based network structures, which we call Categorical Graph Neural Networks (CaGNN). Over a query categorization dataset of 2k categories and another ad title categorization dataset of 5k categories, CaGNN improves performance significantly compared to a baseline Deep Neural Network model without the CaGNN structure. Notably, top 3 prediction recall increases from 90.15% to 91.40% for the ad title categorization task, for which is quite significant at over 90% level for more than 5k categories. By inspecting the learned category embeddings and the flow of message passing, we show that CaGNN effectively encapsulates useful graph structural information. Online A/B testing result shows that an ad ranking model with CaGNN-based features has increased ad click-through rate by 1.81% and reduced defect rate by 2.64%. The model has been deployed to production.
-
Coordinated Motion Planning Through Randomized k-OptJack Spalding-Jamieson, Paul Liu, Brandon Zhang, Da Wei Zheng
[pdf] [code]
This paper describes the heuristics and algorithms used by team gitastrophe in the CG:SHOP 2021 Competition. The contest was run in two categories with different optimization objectives: SUM and MAX. Team gitastrophe placed first overall in the SUM category, third overall in the MAX category, and first among junior teams for both categories.
-
Elo-MMR: A Rating System for Massive Multiplayer CompetitionsAram Ebtekar and Paul Liu
[pdf] [code] [data]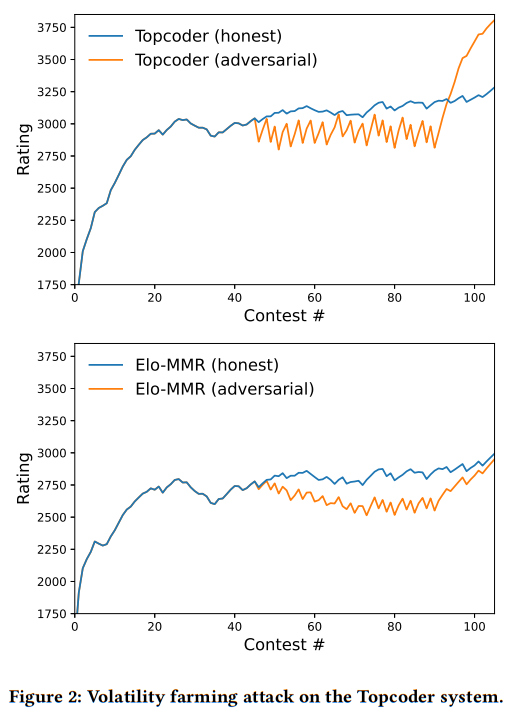
Skill estimation mechanisms, colloquially known as rating systems, play an important role in competitive sports and games. They provide a measure of player skill, which incentivizes competitive performances and enables balanced match-ups. In this paper, we present a novel Bayesian rating system for contests with many participants. It is widely applicable to competition formats with discrete ranked matches, such as online programming competitions, obstacle courses races, and video games. The system's simplicity allows us to prove theoretical bounds on its robustness and runtime. In addition, we show that it is incentive-compatible: a player who seeks to maximize their rating will never want to underperform. Experimentally, the rating system surpasses existing systems in prediction accuracy, and computes faster than existing systems by up to an order of magnitude.
-
Diversity on the Go! Streaming Determinantal Point Processes under a Maximum Induced Cardinality ObjectivePaul Liu, Akshay Soni, Eun Yong Kang, Yajun Wang, Mehul Parsana
[pdf] [code]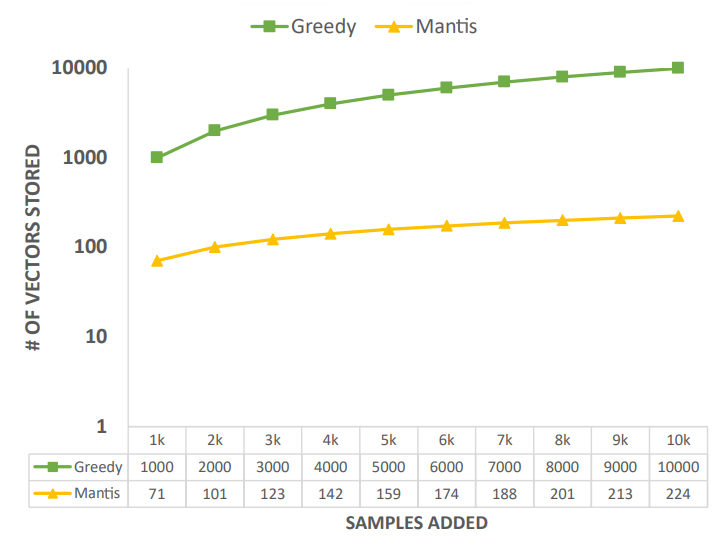
Over the past decade, Determinantal Point Processes (DPPs) have proven to be a mathematically elegant framework for modeling diversity. Given a set of items $N$, DPPs define a probability distribution over subsets of $N$, with sets of larger diversity having greater probability. Recently, DPPs have achieved success in the domain of recommendation systems, as a method to enforce diversity of recommendations in addition to relevance.
In large-scale recommendation applications however, the input typically comes in the form of a stream too large to fit into main memory. However, the natural greedy algorithm for DPP-based recommendations is memory intensive, and cannot be used in a streaming setting.
In this work, we give the first streaming algorithm for optimizing DPPs under the Maximum Induced Cardinality (MIC) objective of Gillenwater et al. As noted by Gillenwater et al., the MIC objective is better suited towards recommendation systems than the classically used maximum a posteriori (MAP) DPP objective. In the insertion-only streaming model, our algorithm runs in $\tilde{O}(k^2)$ time per update and uses $\tilde{O}(k)$ memory, where $k$ is the number of diverse items to be selected. In the sliding window streaming model, our algorithm runs in $\tilde{O}(\sqrt{n}k^2)$ time per update and $\tilde{O}(\sqrt{n}k)$ memory where $n$ is the size of the sliding window. The approximation guarantees are simple, and depend on the largest and the $k$-th largest eigenvalues of the kernel matrix used to model diversity. We show that in practice, the algorithm often achieves close to optimal results, and meets the memory and latency requirements of production systems. Furthermore, the algorithm works well even in a non-streaming setting, and runs in a fraction of time compared to the classic greedy algorithm.
-
Improved Algorithms for Edge Colouring in the W-Streaming ModelPaul Liu and Moses Charikar
[pdf] [slides] [video]In the W-streaming model, an algorithm is given $O(n \text{polylog} n)$ space and must process a large graph of up to $O(n^2)$ edges. In this short note we give two algorithms for edge colouring under the W-streaming model. For edge colouring in W-streaming, a colour for every edge must be determined by the time all the edges are streamed. Our first algorithm uses $\Delta+o(\Delta)$ colours in $O(n \log^2 n)$ space when the edges arrive according to a uniformly random permutation. The second algorithm uses $(1+o(1))\Delta^2/s$ colours in $\tilde{O}(ns)$ space when edges arrival adversarially.
2020
-
Retrieving Top Weighted Triangles in GraphsRaunak Kumar*, Paul Liu*, Moses Charikar, Austin Benson
[pdf] [code] [poster] [slides]
Pattern counting in graphs is a fundamental primitive for many network analysis tasks, and a number of methods have been developed for scaling subgraph counting to large graphs. Many real-world networks carry a natural notion of strength of connection between nodes, which are often modeled by a weighted graph, but existing scalable graph algorithms for pattern mining are designed for unweighted graphs. Here, we develop a suite of deterministic and random sampling algorithms that enable the fast discovery of the 3- cliques (triangles) with the largest weight in a graph, where weight is measured by a generalized mean of a triangle’s edges. For example, one of our proposed algorithms can find the top-1000 weighted triangles of a weighted graph with billions of edges in thirty seconds on a commodity server, which is orders of magnitude faster than existing “fast” enumeration schemes. Our methods thus open the door towards scalable pattern mining in weighted graphs.
-
A Polynomial Lower Bound on Adaptive Complexity of Submodular MaximizationWenzheng Li, Paul Liu, Jan Vondrák
[pdf] [slides] [video]
Informally, the adaptive model measures complexity by the longest chain of sequentially dependent calls to $f$ in the algorithm. The focus of the adaptive model is to reward highly parallel algorithms, and penalize algorithms that have high 'sequentiality'. Much work has been devoted recently to creating efficient algorithms for submodular optimization (SUBMOD) in the adaptive model. We focus instead on the lower bound, and provide the first lower bound showing that any approximation for monotone SUBMOD takes polynomially many rounds as the approximation factor approaches $1-1/e$.
For the unconstrained non-monotone maximization problem, we show a positive result. For every instance, and every $\delta> 0$, either we obtain a $(1/2-\delta)$-approximation in 1 round, or a $(1/2 + \Omega(\delta^2))$-approximation in $O(1/\delta^2)$ rounds. Unlike the cardinality-constrained case, there cannot be an instance where (i) it is impossible to achieve an approximation factor better than $1/2$ regardless of the number of rounds, and (ii) it takes $r$ rounds to achieve a factor of $1/2 − O(1/r)$.
2019
-
Submodular Optimization in the MapReduce ModelPaul Liu and Jan Vondrák
[pdf]
Submodular optimization has received significant attention in both practice and theory, as a wide array of problems in machine learning, auction theory, and combinatorial optimization have submodular structure. In practice, these problems often involve large amounts of data, and must be solved in a distributed way. One popular framework for running such distributed algorithms is MapReduce. In this paper, we present two simple algorithms for cardinality constrained submodular optimization in the MapReduce model: the first is a $(1/2 - o(1))$-approximation in 2 MapReduce rounds, and the second is a $(1 - 1/e - \epsilon)$-approximation in $\frac{1+o(1)}{\epsilon}$ MapReduce rounds.
-
Sampling Methods for Counting Temporal MotifsPaul Liu, Austin Benson, Moses Charikar
[pdf] [code] [poster] [slides]
Subgraph isomorphism is a classic and well studied problem in computer science. However, modern graph datasets now contain richer structure, and incorporating temporal information in particular has become a key part of network analysis. In this work we develop fast sampling algorithms for temporal motif counting (subgraph isomorphism where the subgraph must have edges appearing in a specific order). Our results show that we can achieve one to two orders of magnitude speedup over existing algorithms with minimal and controllable loss in accuracy on a number of datasets.
2018
-
Greedy and Local Ratio Algorithms in the MapReduce ModelNicholas J. A. Harvey, Christopher Liaw, Paul Liu
[pdf] [slides]
MapReduce has become the de facto standard model for designing distributed algorithms to process big data on a cluster. There has been considerable research on designing efficient MapReduce algorithms for clustering, graph optimization, and submodular optimization problems. We develop new techniques for designing greedy and local ratio algorithms in this setting. Our randomized local ratio technique gives 2-approximations for weighted vertex cover and weighted matching, and an $f$-approximation for weighted set cover, all in a constant number of MapReduce rounds. Our randomized greedy technique gives algorithms for maximal independent set, maximal clique, and a $(1+\epsilon)\log \Delta$-approximation for weighted set cover. We also give greedy algorithms for vertex colouring with $(1+o(1))\Delta$ colours and edge colouring with $(1+o(1))\Delta$ colours.
-
Approximation Schemes for Covering and Packing in the Streaming ModelChristopher Liaw, Paul Liu, Robert Reiss
[pdf]
Within the computational geometry (CG) community, the shifting strategy is a popular algorithmic paradigm for approximation algorithms. In this work we revisit the shifting strategy in the streaming model. Using the streaming-shifting strategy, we give low-memory approximation algorithms for classical CG problems such as unit disc cover. When combined with the shifting coreset technique of Fonseca et al., we are able to approximate streaming variants of geometric dominating set, independent set, etc.
2017
-
SYM-ILDL: Incomplete $LDL^T$ Factorization of Symmetric Indefinite and Skew-Symmetric MatricesChen Greif, Paul Liu, Shiwen He
[pdf] [code]
SYM-ILDL is a numerical software package that computes incomplete $LDL^T$ (or `ILDL') factorizations of symmetric indefinite and real skew-symmetric matrices. The core of the algorithm is a Crout variant of incomplete LU (ILU), originally introduced and implemented for symmetric matrices by [Li and Saad, Crout versions of ILU factorization with pivoting for sparse symmetric matrices, Transactions on Numerical Analysis 20, pp. 75--85, 2005]. Our code is economical in terms of storage and it deals with real skew-symmetric matrices as well, in addition to symmetric ones. The package is written in C++ and it is templated, open source, and includes a MATLAB interface. The code includes built-in RCM and AMD reordering, two equilibration strategies, threshold Bunch-Kaufman pivoting and rook pivoting, as well as a wrapper to MC64, a popular matching based equilibration and reordering algorithm. We also include two built-in iterative solvers: SQMR preconditioned with ILDL, or MINRES preconditioned with a symmetric positive definite preconditioner based on the ILDL factorization.
-
Approximation Algorithms for the Unit Disk Cover Problem in 2D and 3DAhmad Biniaz, Paul Liu, Anil Maheshwari, Michiel Smid
[pdf]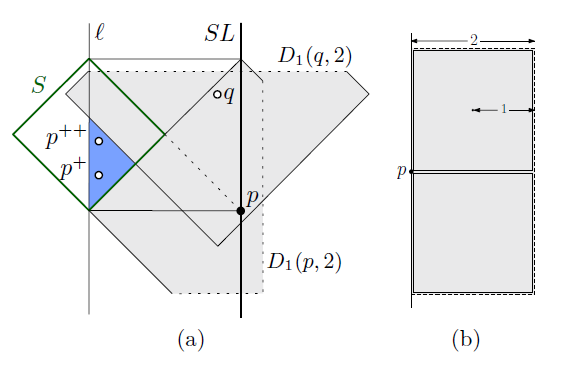
Given a set P of n points in the plane, we consider the problem of covering P with a minimum number of unit disks. This problem is known to be NP-hard. We present a simple 4-approximation algorithm for this problem which runs in $O(n \log n)$-time. We also show how to extend this algorithm to other metrics, and to three dimensions.
2016
-
Characterizing Minimum-Length Coordinated Motions for Two DiscsDavid Kirkpatrick and Paul Liu
[pdf]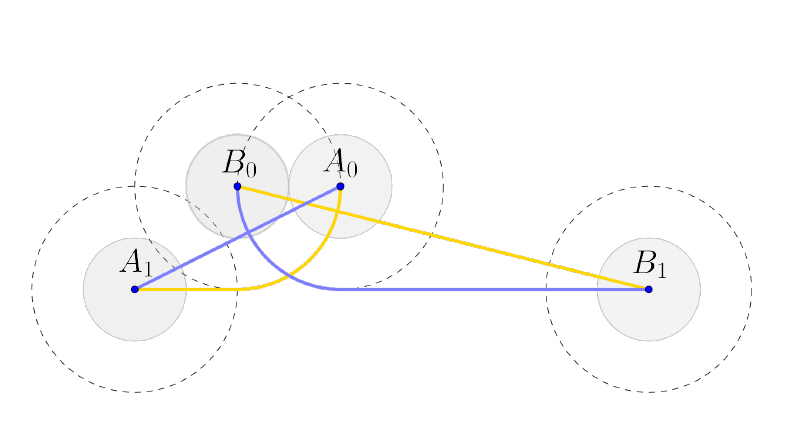
We study the problem of planning coordinated motions for two disc robots in an otherwise obstacle-free plane. We give a characterization of collision-avoiding motions that minimize the total trace length of the disc centres, for all initial and final configurations of the robots. The individual traces are composed of at most six (straight or circular-arc) segments, and their total length can be expressed as a simple integral with a closed form solution depending only on the initial and final configuration of the robots.
2014
-
A Fast 25/6-approximation for the Minimum Unit Disk Cover ProblemPaul Liu, Daniel Lu
[pdf]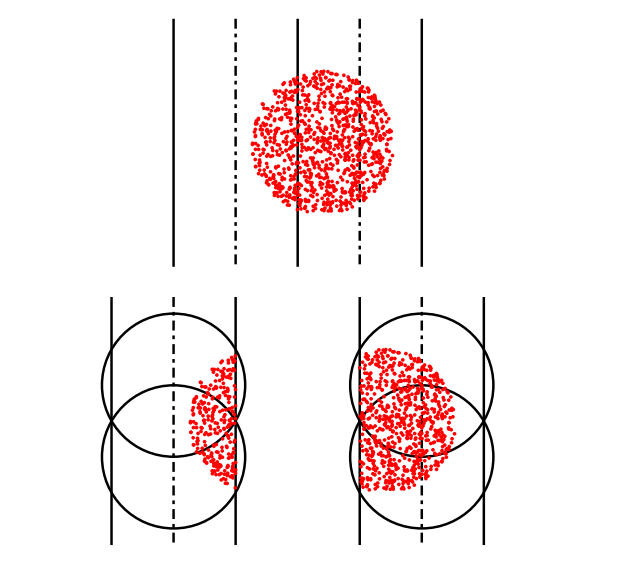
My very first paper!
Given a point set in 2D, what is the minimum number of unit radius discs that covers all of the points? This is called the Unit Disk Cover (UDC) problem and has a wide variety of applications in facility location, motion planning, and image processing. Unfortunately, UDC is also NP-Hard.
In this work we present simple and practical $25/6$-approximation algorithms for UDC with runtime $O(n \log n)$ and space $O(n)$. This algorithm additionally extends to discs in any $\ell_p$ norm.