computational geometry
-
Coordinated Motion Planning Through Randomized k-OptJack Spalding-Jamieson, Paul Liu, Brandon Zhang, Da Wei Zheng
[pdf] [code]
This paper describes the heuristics and algorithms used by team gitastrophe in the CG:SHOP 2021 Competition. The contest was run in two categories with different optimization objectives: SUM and MAX. Team gitastrophe placed first overall in the SUM category, third overall in the MAX category, and first among junior teams for both categories.
-
Approximation Schemes for Covering and Packing in the Streaming ModelChristopher Liaw, Paul Liu, Robert Reiss
[pdf]
Within the computational geometry (CG) community, the shifting strategy is a popular algorithmic paradigm for approximation algorithms. In this work we revisit the shifting strategy in the streaming model. Using the streaming-shifting strategy, we give low-memory approximation algorithms for classical CG problems such as unit disc cover. When combined with the shifting coreset technique of Fonseca et al., we are able to approximate streaming variants of geometric dominating set, independent set, etc.
-
Approximation Algorithms for the Unit Disk Cover Problem in 2D and 3DAhmad Biniaz, Paul Liu, Anil Maheshwari, Michiel Smid
[pdf]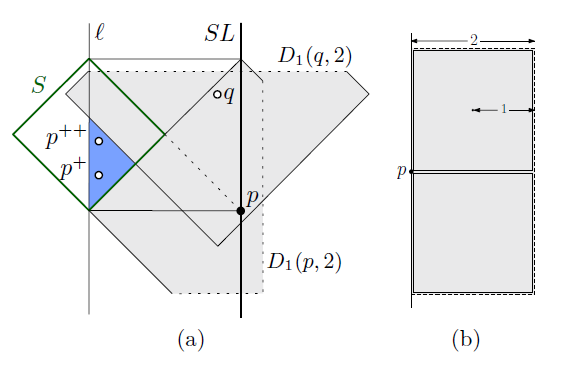
Given a set P of n points in the plane, we consider the problem of covering P with a minimum number of unit disks. This problem is known to be NP-hard. We present a simple 4-approximation algorithm for this problem which runs in $O(n \log n)$-time. We also show how to extend this algorithm to other metrics, and to three dimensions.
-
Characterizing Minimum-Length Coordinated Motions for Two DiscsDavid Kirkpatrick and Paul Liu
[pdf]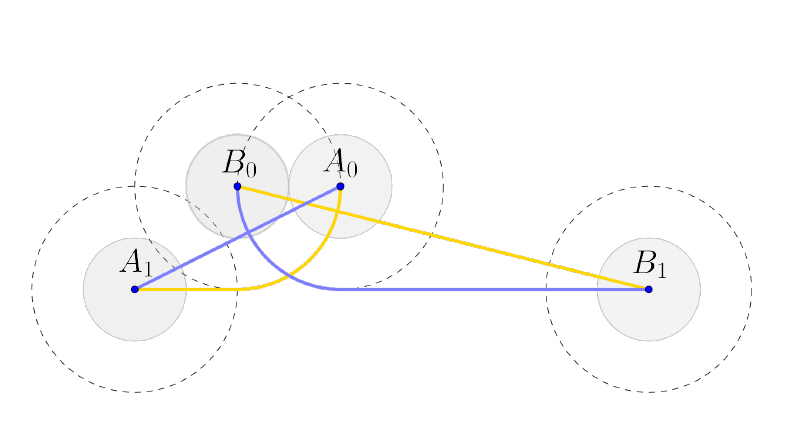
We study the problem of planning coordinated motions for two disc robots in an otherwise obstacle-free plane. We give a characterization of collision-avoiding motions that minimize the total trace length of the disc centres, for all initial and final configurations of the robots. The individual traces are composed of at most six (straight or circular-arc) segments, and their total length can be expressed as a simple integral with a closed form solution depending only on the initial and final configuration of the robots.
-
A Fast 25/6-approximation for the Minimum Unit Disk Cover ProblemPaul Liu, Daniel Lu
[pdf]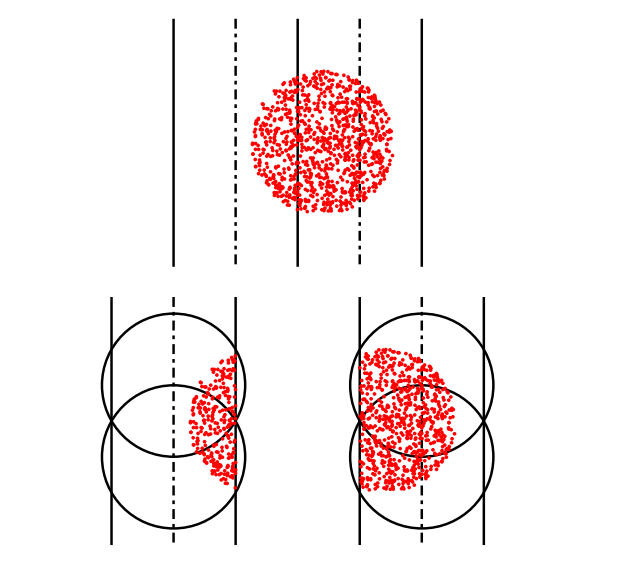
My very first paper!
Given a point set in 2D, what is the minimum number of unit radius discs that covers all of the points? This is called the Unit Disk Cover (UDC) problem and has a wide variety of applications in facility location, motion planning, and image processing. Unfortunately, UDC is also NP-Hard.
In this work we present simple and practical $25/6$-approximation algorithms for UDC with runtime $O(n \log n)$ and space $O(n)$. This algorithm additionally extends to discs in any $\ell_p$ norm.