ConvNetJS
Deep Learning in your browser
Brief intro to Deep Learning: Digit Classification Example
Several large companies (Google, Facebook, Microsoft, Baidu) now use Deep Learning models for various Machine Learning tasks, most notably and successfully speech and image recognition, and slowly natural language processing. Read more.
Lets use the special case of image classification as a working example. Deep Learning is about stacking different types of transformers (layers) on top of each other. Like when you make a sandwich. Unlike a sandwich however, each layer accepts a volume of numbers (we like to call them activations since we think of each number as a firing rate of a neuron) and transforms it into a different volume of numbers using some set of internal parameters (we like to think of those as trainable synapses).
In the simplest and most traditional setup, the first volume of activations represents your input and the last volume represents probabilities of the input volume being among any one of several distinct classes. During training you provide the network many examples of pairs of (input volume, class) and the network tunes its parameters ("learns") to transform inputs into correct class probabilities.
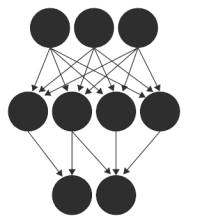
Here's an MNIST digits example: suppose we have an image (a 28x28 array of pixel values) that contains a 4. We create a 2D volume of size (28,28) and fill it with the pixel values. Then we pipe the input volume through the network and get output volume of 10 numbers representing the probability that the input is any one of 10 different digits:

So we transformed the original image into probabilities (taking many intermediate forms of representation along the way (that's the gray boxes in my artistic rendering). Every box is a 3-dimensional array of numbers). But wait, it looks like the network only assigned 10 percent probability to this input being a 4, and 60 percent to it being a 9! That's fine: by design the mapping from input to output is a mathematical function that is parameterized by some numbers and we can tune these parameters to make the network slightly more likely to give class 4 a higher probability for this particular input in the future.
The details require a bit of calculus, but you can write down the expression for the probability of digit 4 for this particular input (this is what we wish to increase) and differentiate it to derive the expression for the gradient with respect to all of network's parameters. The gradient is the vector in the parameter space along which your function (here probability of 4) increases the most. So we forwarded our image of 4, computed the probability of answer being 4, then computed the gradient on all parameters of the network, and finally we nudge all the parameters slightly along that gradient. Some people call this procedure backpropagation (or backprop), but in the form I presented it's also just stochastic gradient descent, a vanilla method in optimization literature.
The amount we nudge is called the learning rate, and is perhaps the single most important number in training these networks. If it's high, the networks learn faster, but if it's too high, the networks can explode. On the other hand, if it's too low the training will take a very long time. Usually you start it higher (for example say 0.1), but not too high (!) and anneal it slowly over time a few orders of magnitude (down to 0.0001 perhaps).
In any case, what it comes down to is that after the nudge the network will be a tiny bit more likely to predict a 4 on this image. So we just start from some random parameters, repeat this procedure for tens of thousands of different digits, and the network gradually transforms itself into a digit classifier.
External Resources
Here are some more resource recommendations, ordered from beginner to advanced:
- Michael Nielsen's Chapter 1 seems like a nice and gentle introduction to neural networks.
- CS231n class at Stanford has both slides and lecture videos on YouTube.
- Andrew Ng's CS229 and the Coursera class are a great resource for Machine Learning, even if they do not explicitly cover Neural Networks.
- UFLDL tutorials for a set of nice Matlab exercises.
- Chris Manning has a nice (but slightly more mathematically demanding and Natural Language Processing focused) set of videos here
- Hugo Larochelle's nice, but fairly advanced class on Machine Learning (Neural Nets included). Note that the page is in French but the slides and videos are in English.
- deepLearning.net has a ton of other resources listed.
