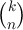 . Thus the count we
want is given by
. Thus the count we
want is given by
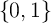 n = x0x1
n = x0x1 xn-1,
define digitsum(x) = ∑
ixi as the number of 1s in x. We want
to know the number of bit strings that have digitsum(x) ≡ 0(
mod3).
xn-1,
define digitsum(x) = ∑
ixi as the number of 1s in x. We want
to know the number of bit strings that have digitsum(x) ≡ 0(
mod3).
For 0 ≤ k ≤ n, the number of bit strings with digitsum(x) = k
is given by the binomial co-efficient 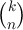 . Thus the count we
want is given by
. Thus the count we
want is given by
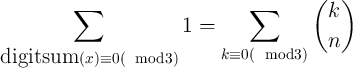
Consider the primitive cube root of 1, ω = -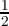 +
+ 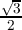 i.
Since ω2 = -
i.
Since ω2 = -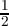 -
-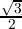 i and ω3 = 1, we have the real part
ℜ(ωk) = 1 if k ≡ 0( mod3) and -
i and ω3 = 1, we have the real part
ℜ(ωk) = 1 if k ≡ 0( mod3) and -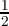 otherwise. We can
scale this to get a function of k which is 1 for k divisible
by 3 and 0 otherwise, i.e. with f(k) =
otherwise. We can
scale this to get a function of k which is 1 for k divisible
by 3 and 0 otherwise, i.e. with f(k) = 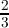 ℜ(ωk) +
ℜ(ωk) + 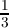 , we
have
, we
have
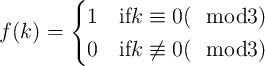
Thus, the count is
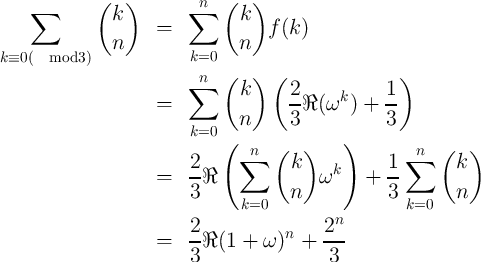
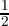 +
+ 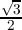 is the primitive sixth root of 1, and we
have ℜ(1 + ω)n = 1,
is the primitive sixth root of 1, and we
have ℜ(1 + ω)n = 1,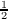 ,-
,-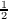 ,-1,-
,-1,-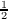 ,
,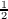 respectively, based on n(
mod3) ≡ 0, 1, 2, 3, 4, 5. Substituting in the above equation,
our count =
respectively, based on n(
mod3) ≡ 0, 1, 2, 3, 4, 5. Substituting in the above equation,
our count = 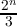 ±
± 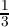 or
or 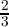 . The counts for
digitsum(x) ≡ 1 or 2( mod3) is similar except that we use
ωk+2 or ωk+1 in the equation. This gives us the final
table:
. The counts for
digitsum(x) ≡ 1 or 2( mod3) is similar except that we use
ωk+2 or ωk+1 in the equation. This gives us the final
table:
| n mod3 | 0 | 1 | 2 | 3 | 4 | 5 |
count(digitsum(x) ≡ 0( mod3)) = 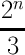 + + | 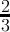 | 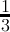 | -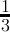 | -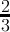 | -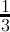 | 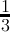 |
count(digitsum(x) ≡ 1( mod3)) = 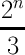 + + | -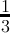 | 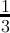 | 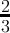 | 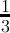 | -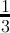 | -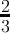 |
count(digitsum(x) ≡ 2( mod3)) = 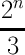 + + | -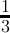 | -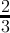 | -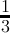 | 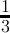 | 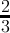 | 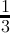 |
Anil Das