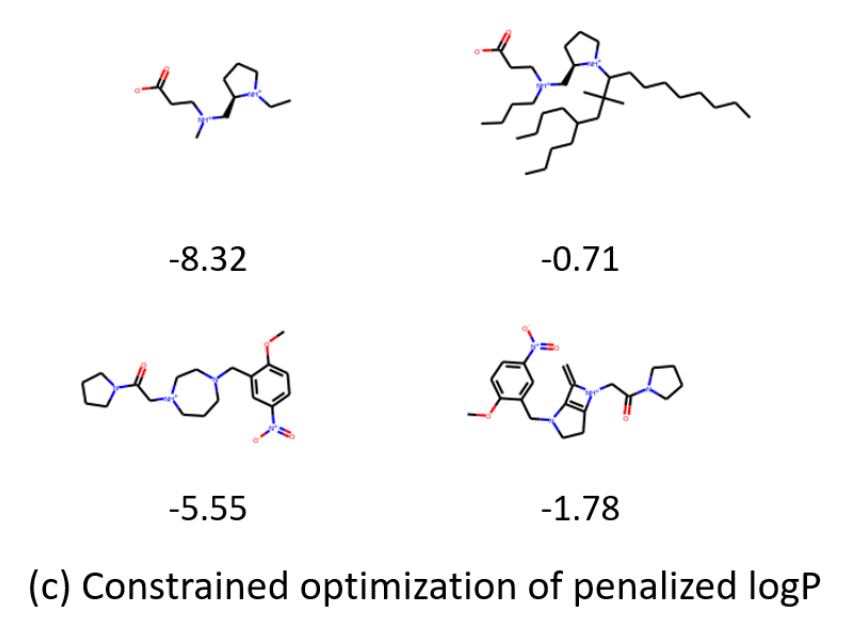
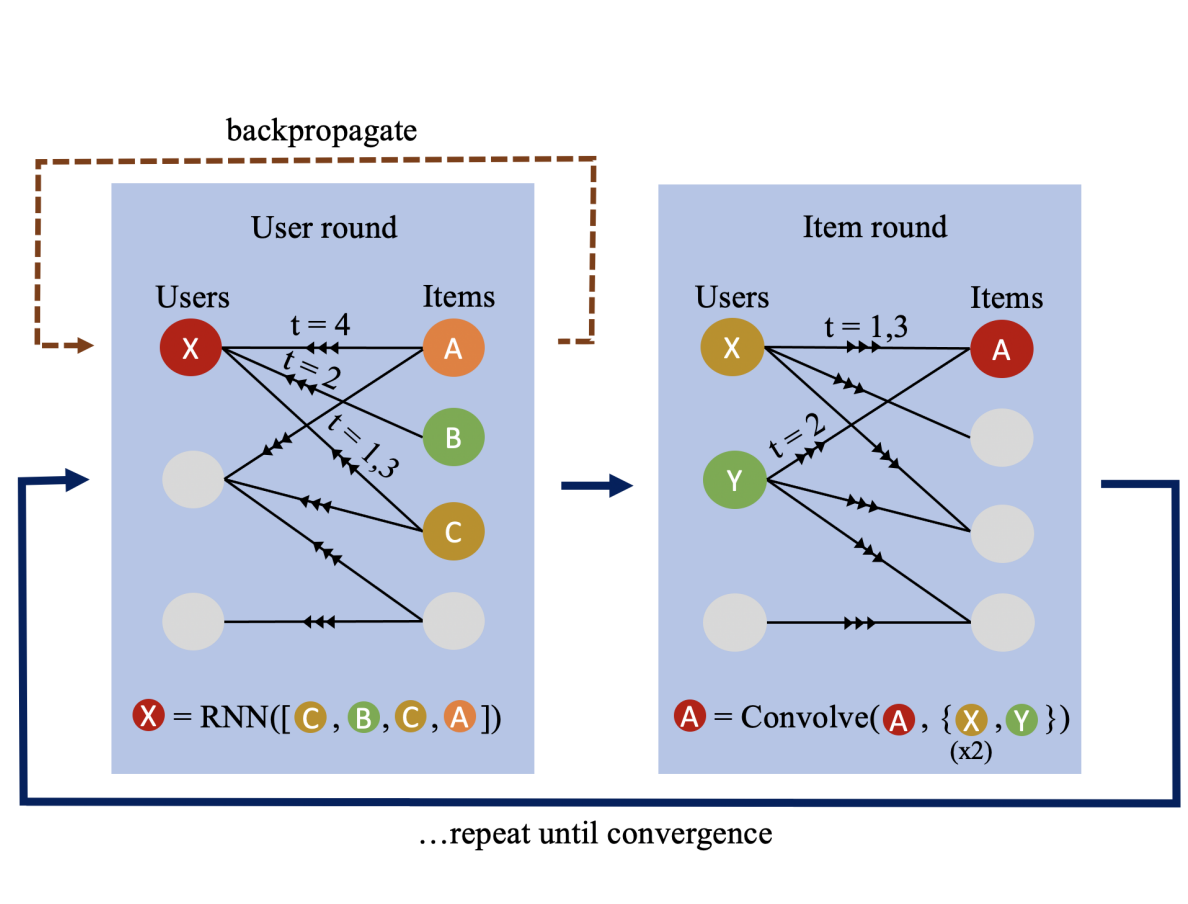
Deep Learning on Graphs
I focus on advancing graph neural network (GNN) architectures and improving the expressiveness, scalability, interpretability and robustness of GNNs.
ICML 2022
LA-GNN is a general pre-training framework that improves GNN performance through augmentation.ICLR 2021
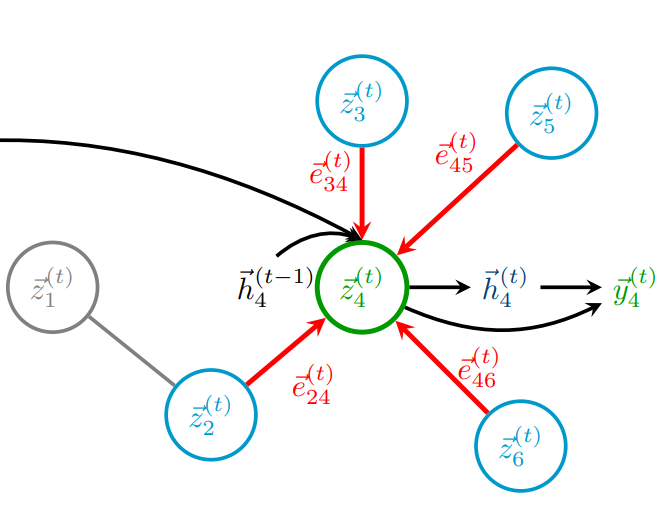
GNNs can learn to execute graph algorithms.AAAI 2021
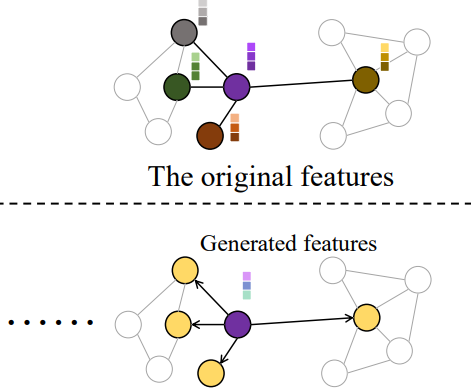
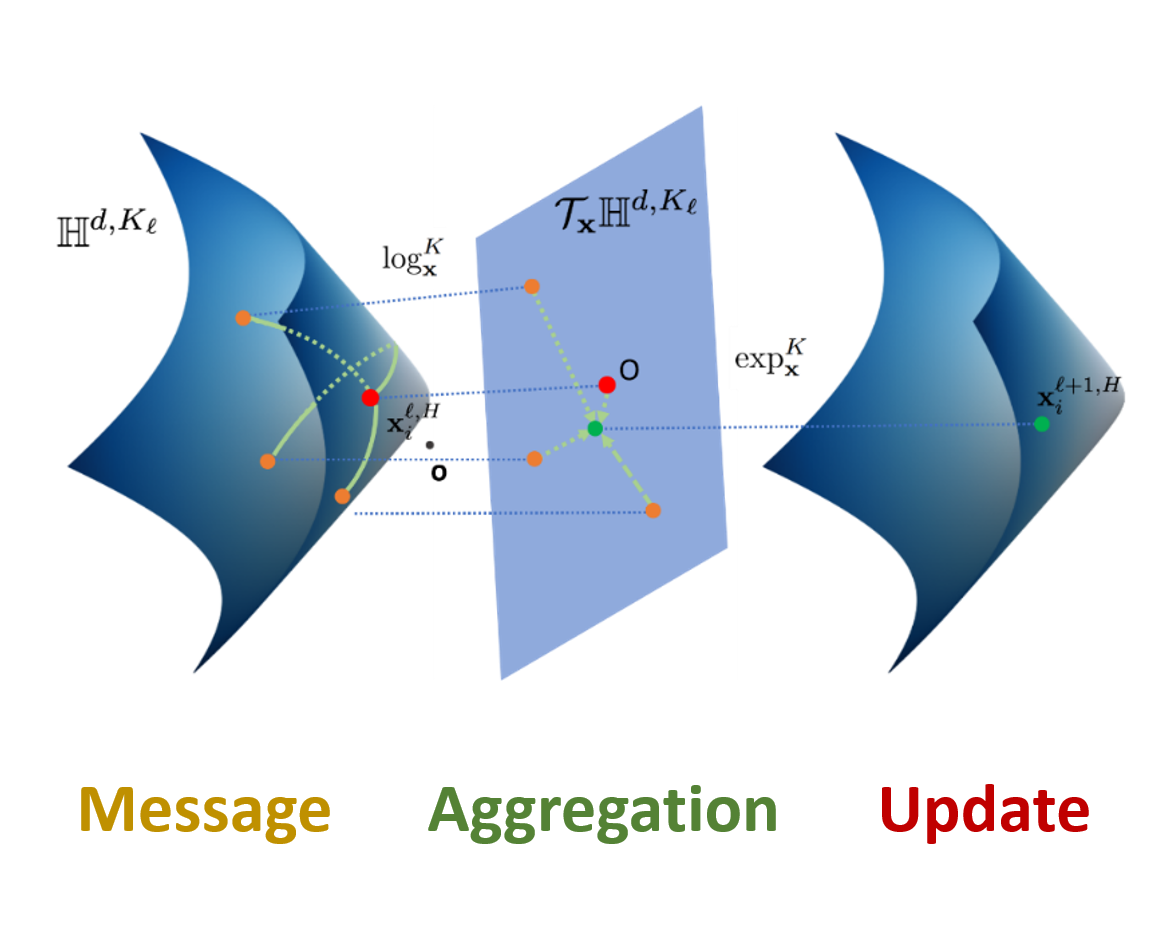
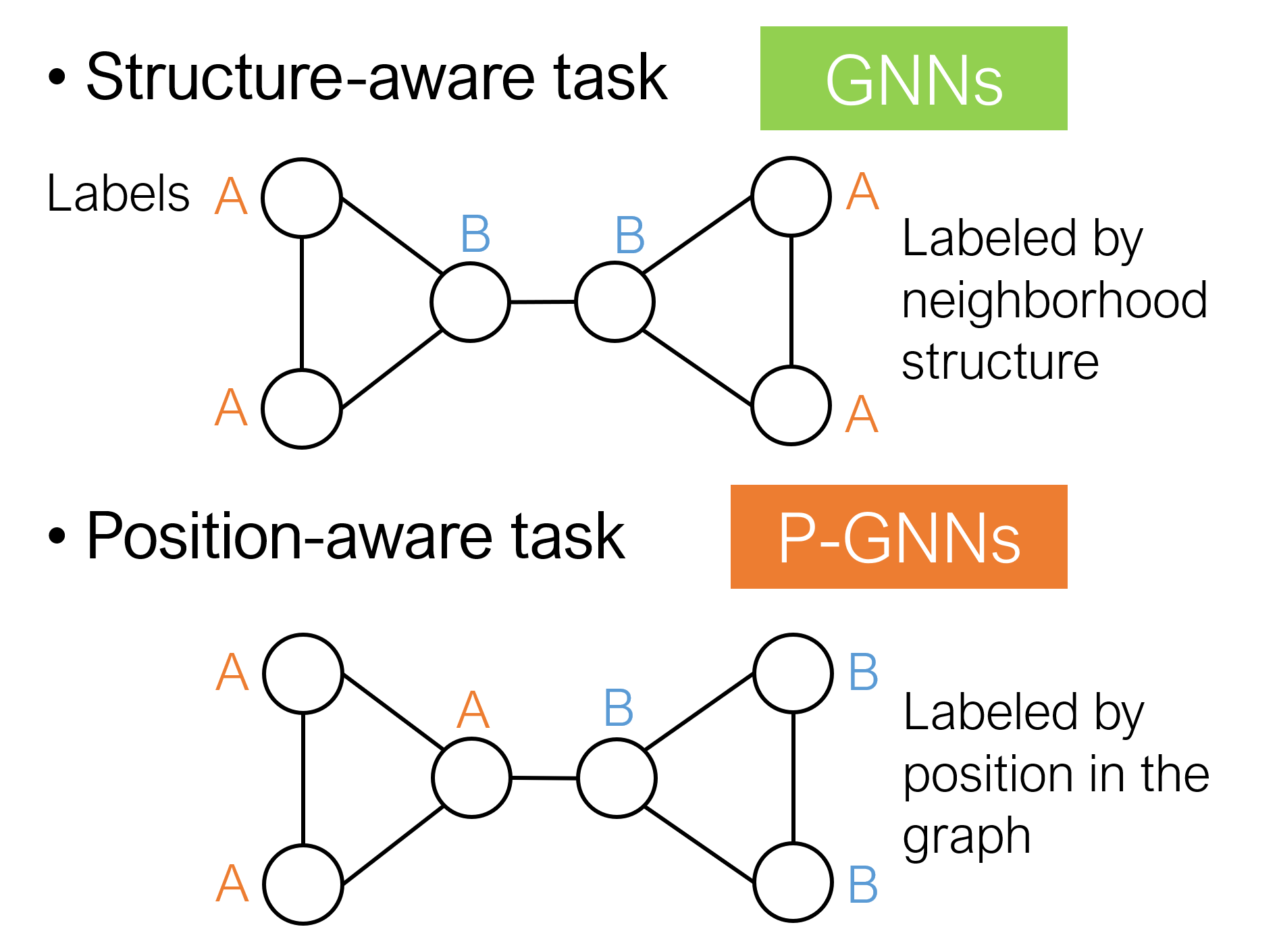
ID-GNN improves the expressiveness of GNN by considering node identities.NeurIPS 2017
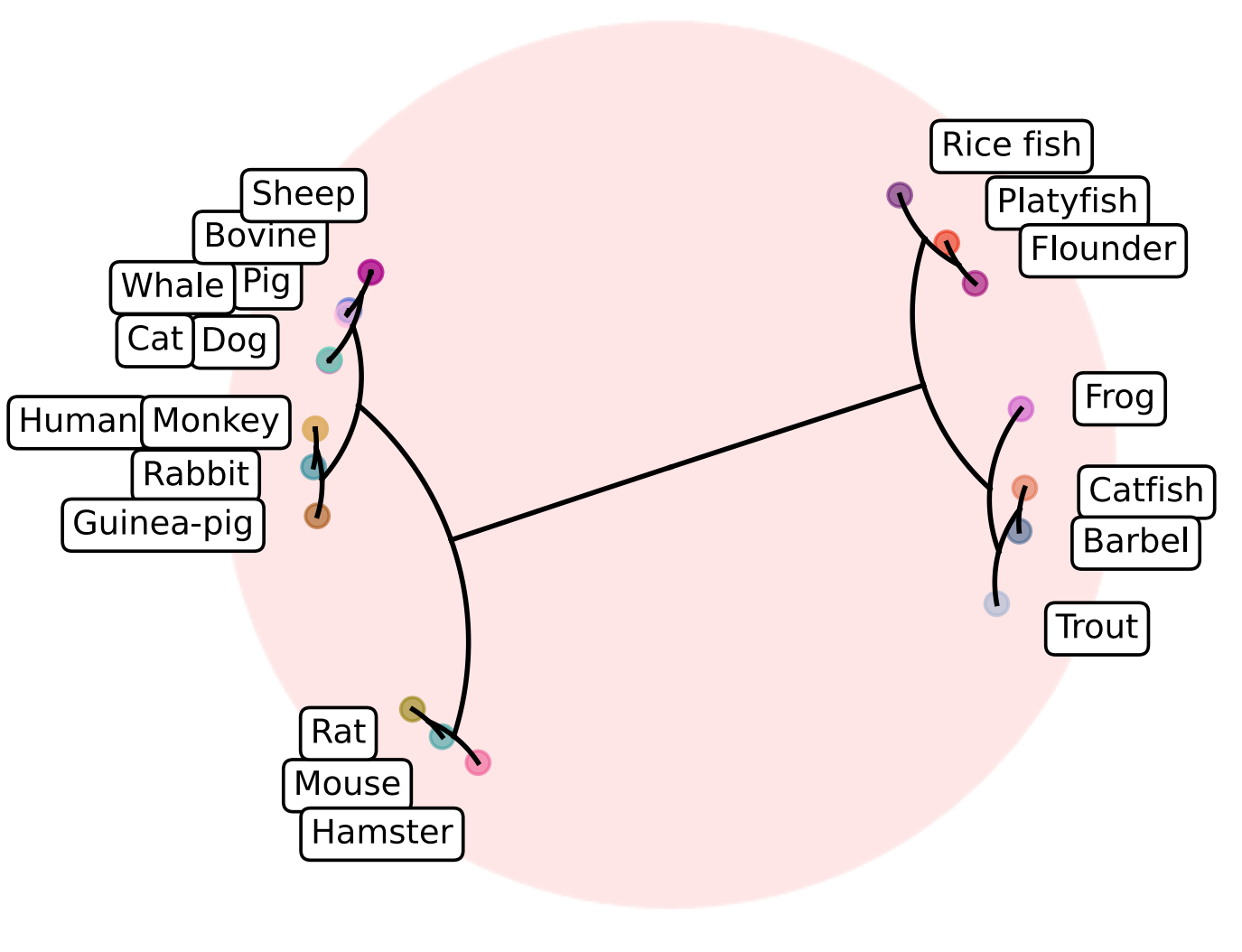
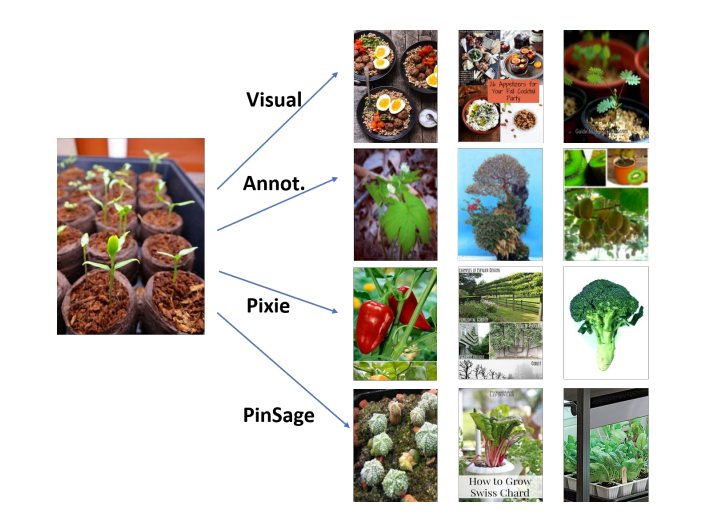
GraphSAGE is a general GNN framework for large-scale graph learning.ICML 2018
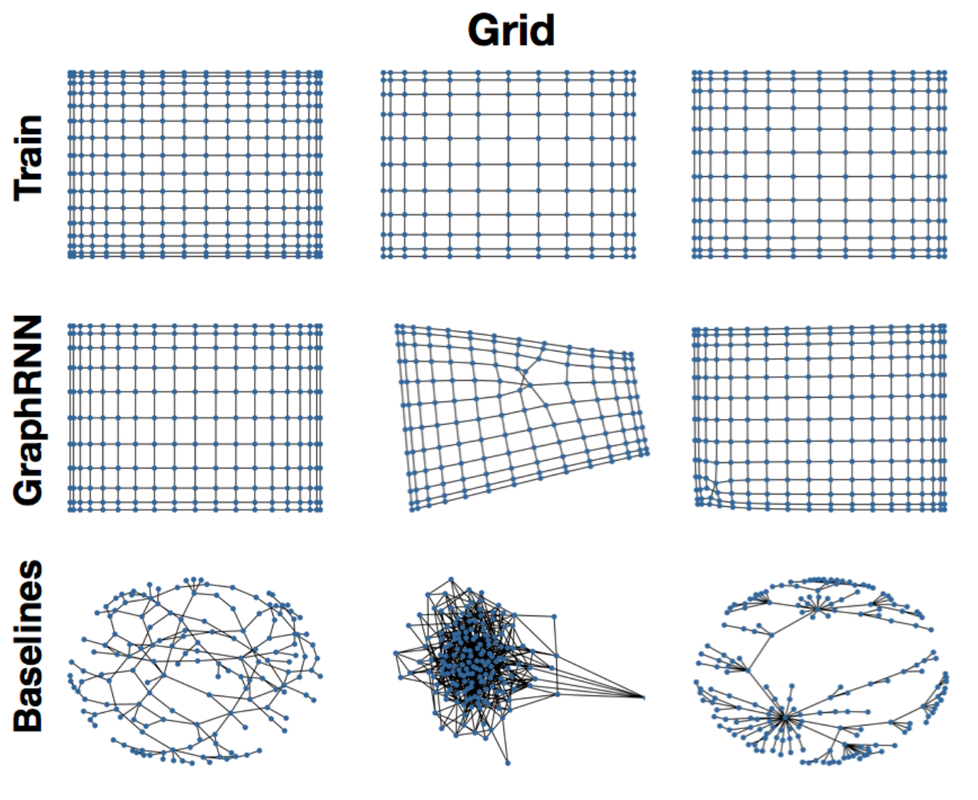
GraphRNN is one of the first graph generative models for learning distribution of graphs.NeurIPS 2019
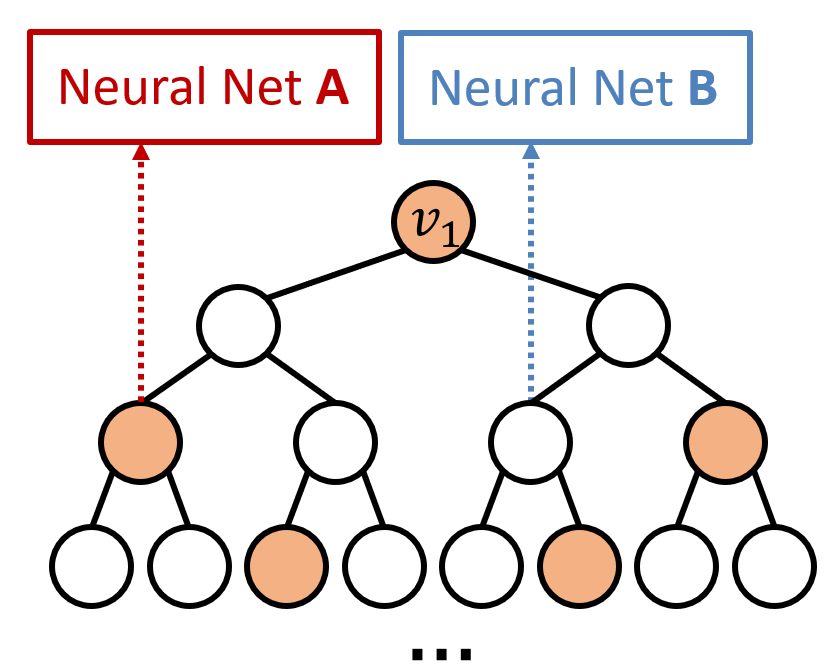
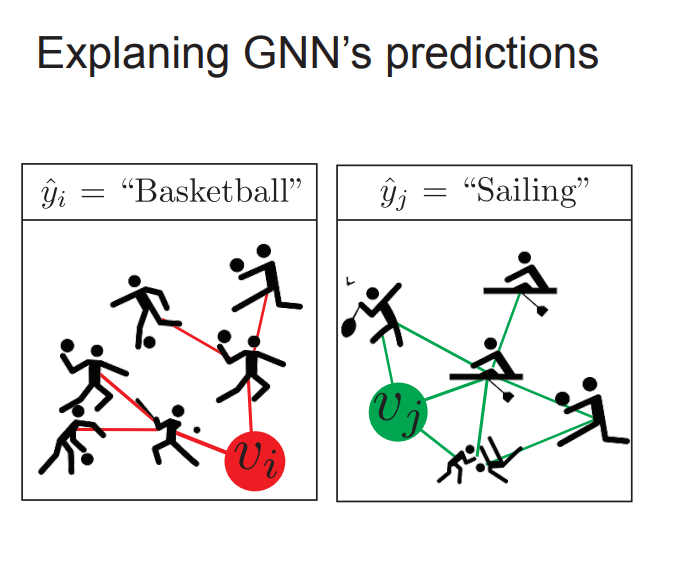
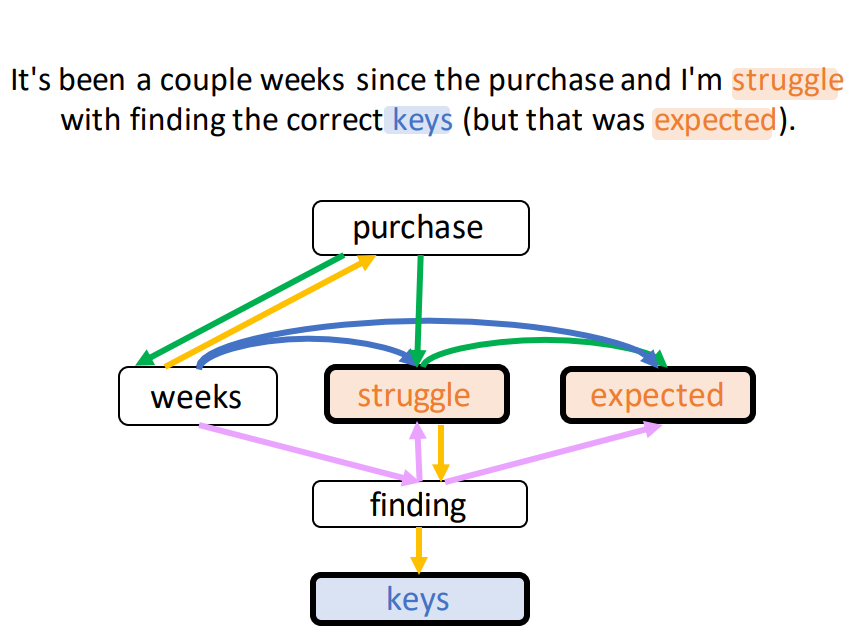
The first framework to explain predictions made by GNNs!