Chapter 7
Object-Oriented Graphics
One of the most widely cited problems in teaching Java—identified as problem A1 in the taxonomy from Chapter 2—is the lack of a graphics facility that is simple enough for novices to use. This problem has been identified as critical by several authors [Bruce01, Martin98, Roberts98]; Nick Parlante goes so far as to suggest that it is the only problem that rises above his critical threshold:
Java has many little features that I thought might be a problem in CS1, but in almost every case they worked out fine. Graphics was the one exception. [Parlante04a]
Given the perceived importance of the problem, we were not surprised to find that graphical packages were heavily represented among the solution strategies submitted to the Java Task Force. These packages fall into three categories:
- Object-based packages in which the user creates objects that draw themselves in a window [Bruce04a, Parlante04a, SandersK04a, SandersK04b]
- Packages that offer a traditional Cartesian-based graphical model [Roberts04e]
- Packages that present graphics in the context of a “microworld” [Lambert04b, SandersD04a]
After discussing these strategies at a task force meeting, we decided to pursue only the first approach. Teaching students a graphics model that differs from Java’s in any substantive way runs the risk of confusing them all the more when they start to use the facilities in the standard Java packages. And although microworlds can have significant pedagogical value, they seem to fall outside the scope of the task force charge. For the most part, such packages are stand-alone and can be adopted easily even if the Java Task Force does not include them in its collection of libraries. There are, moreover, many existing microworld approaches, and it would serve no educational purpose to privilege a particular microworld design.
We were, however, convinced of the value of supporting a simple, object-based graphics facility that allows students to assemble figures by creating a graphical canvas and then adding graphical objects to it. The advantages of having such a package include:
- It enables students to use graphics from the very beginning of the first course. Students today, having grown up with graphical interfaces, are much more interested in this type of program than they are in the more traditional input/process/output style of program.
- An object-based graphics model simplifies enormously the task of responding to repaint requests. In both the Abstract Windowing Toolkit (AWT) and the more powerful model provided by Swing, the programmer is responsible for repainting the contents of a window whenever an update is necessary. Implementing that repaint operation under the standard graphics model forces students to maintain enough state information to regenerate the display, which typically requires some sophistication with data structures. Graphical objects, however, are designed so that they repaint themselves, thereby automating the repaint process.
- A graphical object hierarchy provides a compelling illustration of how object-oriented programming works. If the package is well designed, it can serve as an early illustration of general notions like subclassing and inheritance along with more specific implementation strategies such as abstract classes and interfaces. The desire to use the graphics class hierarchy as a pedagogical tool provides a strong incentive to keep the package small and consistent in its design.
Although we were convinced that an object-based graphics package had to one of our deliverables, none of the submissions in response to our call for proposals was in fact ideal. Each of these proposals has strengths and weaknesses, as outlined in Figure 7-1. The proposals therefore served as a foundation for the design of a new package that incorporates the best features of each. The result of that design effort is the acm.graphics package, which defines an extensible hierarchy of graphical objects rooted at the GObject class. The subsections that follow offer an overview of acm.graphics and describe the design decisions involved in its development.
Figure 7-1. Strengths and weaknesses of the proposed graphics packages
| | + | Successful experience at multiple institutions |
| + | Clean and consistent animation model |
| + | Sufficient functionality to define interesting pictures |
| | | ± | Mouse events are available through subclassing, but not by using listeners | | |
| – | Package is relatively large (44 classes and interfaces) |
| – | Naming conventions are not consistent |
| – | Class hierarchy is not intuitive (FramedOval extends Rect, for example) |
| – | Drawable classes are not easily extendable by students |
|
|
| | + | Successful experience at multiple institutions |
| + | Reasonably small (20 classes and interfaces of which students use eight) |
| | | ± | Mouse events are available through subclassing, but not by using listeners | | |
| – | Some classes (QuitButton, ConversationBubble) don’t fit the model. |
| – | Some names clash with those in standard libraries (Frame, Image, Shape) |
| – | The package has no general mechanism for displaying strings |
| – | Extending the set of graphical objects requires knowledge of Graphics2D |
|
|
| | + | Successful experience (but only at Stanford) |
| + | Very small (six classes) and easy to learn |
| + | Consistent naming scheme for graphical object classes |
| + | Easily extended by students to create new DShape objects |
| | | ± | Allows composition, but permits non-intuitive containment | | |
| – | Missing some basic functionality, such as drawing lines and arcs |
| – | Rectangles and ovals are always filled, never outlined |
| – | Objects cannot field mouse events |
|
|
|
7.1 The coordinate system
One of the fundamental design decisions in the development of graphics package is the choice of the graphical model, primarily in terms of its coordinate system. Although one of the proposals [Roberts04e] argued for changing the coordinate system to a Cartesian framework similar to that used in Adobe PostScript, the consensus of the task force was that such a model represented too much of a change from the standard Java approach and would therefore force students to learn two incompatible graphics models. We therefore made the decision to stick with a graphics model that for the most part matches that used in the Java AWT: origin in the upper-left corner, y values increasing downward, and coordinates measured in pixels.
| I’m no longer as sure as I was that we need to use doubles to specify coordinates in the client-accessible calls, even though it does make sense to use them internally. Most of the code I’ve written would work just as well using ints, except in the case of the GPolygon and GPen classes, where double-based calls could easily be included without distorting the overall structure. At the very least, I’m convinced that we can abandon the GPoint, GDimension, and GRectangle classes in favor of rounding to the nearest standard AWT class. I looked through all the examples written for MiniJava (which had similar classes) and found no case in which full-precision was important in these compound accessors. I think we need to get a discussion going on this design question. |
There was, however, one change suggested by the proposals that seemed worth adopting. Most of the graphics proposals chose to use real numbers rather than integers in specifying coordinates, at least in the internal model of the coordinate system. The principal advantage is that doing so frees students from having to convert real-valued coordinates—which tend to come up naturally in geometrical calculations, particularly if trigonometric functions or square roots are involved—to their integer equivalents. The idea of rounding coordinates to integers is not that difficult in the abstract, but is complicated by the fact that both rounding functions in the Math class (round and rint) require a cast to produce an int. A more serious problem arises when students make the conversion to integers too early. In such cases, roundoff errors accumulate, leading to polygonal figures that do not close and a host of similar problems.
Allowing real numbers as coordinates has the additional advantage of not forcing adopters to think outside the conceptual box of the Java graphics model. A Java purist who insists that all coordinate variables be declared as integers can still use the acm.graphics package; ints can be passed to methods expecting ints without any problem. The only issue that comes up is that the student must cast the results of methods like getX that return individual coordinates before assigning those values to an integer variable. In practice, those methods are used rarely in programs written by novices.
The decision to use type double for individual coordinates raises the question of how to represent composite coordinate structures like the java.awt classes Point, Dimension, and Rectangle. Since JDK 1.2, double-valued versions of these structures exist in the java.awt.geom package, but the class names (Point2D.Double, Dimension2D.Double, and Rectangle2D.Double) are a bit of a mouthful and expose the notion of inner classes, which is not an introductory-level concept. Several of the proposed packages defined similar real-based classes with simpler names (an early design of the acm.graphics package, for example, defined GPoint, GDimension, and GRectangle), but the inclusion of such classes both expands the package and introduces a nonstandard structure. Such costs are worth paying only if the benefits in providing these classes are significant.
Given typical patterns of use by introductory students, it is unlikely that including new classes to encapsulate real-valued coordinates would be cost-effective. It is much simpler to use the standard Point, Dimension, and Rectangle classes to return composite results in which the coordinate values are rounded internally to the nearest integer. Such an approach seems appropriate for those programs introductory students are likely to write. Moreover, the full-precision coordinates remain available through the individual accessor methods getX, getY, getWidth, and getHeight, in case any client needs access to precise coordinates.
7.2 The graphics class hierarchy
The classes that make up the acm.graphics class hierarchy are shown in Figure 7-2. This section describes why those classes were chosen and why the hierarchy was structured as it is. The fundamental design principles underlying the choices for the class hierarchy are as follows:
- Sufficiency. The classes should provide enough functionality to draw the kind of graphical displays one is likely to encounter in Java. The package should, therefore, include object-based counterparts for those graphical elements that one can produce using the AWT graphics model and should not leave out—as various proposals did—the ability to display lines or strings.
- Transparency. The acm.graphics class hierarchy should be understandable to students and, moreover, should make sense as a paradigmatic example of object-based design. To ensure this goal, the design of the package should avoid the introduction of intermediate classes that would be hard to understand or subclassing relationships that violate the intuitive structure of the model.
- Consistency. All classes in the system should follow a consistent naming scheme and adopt as closely as possible a common operational model.
Figure 7-2. Class diagram for the acm.graphics package
| Scott has argued that we don’t really need G3DRect and GRoundRect. While I agree that they won’t see much use, I think they belong the package for two reasons. First, including them gives us a clear story to tell about why we chose the shape classes we did. Second, these classes offer a useful illustration of multilevel inheritance. |
The central class in the hierarchy shown in Figure 7-2 is the abstract GObject class, which is the common superclass of all graphical objects that can be displayed on a graphical canvas (which is in turn supplied by the GCanvas class described in section 7.4). Descending from GObject is a set of classes—collectively referred to as shape classes—that correspond precisely to the figures one can draw in the original definition of the java.awt.Graphics class. Thus, if the Graphics class includes a draw––– method for some figure –––, the acm.graphics package includes a corresponding GObject subclass with the name G––– (GArc, GImage, GLine, GOval, GPolygon, GRect, GString, GRoundRect, and G3DRect). The two specialized forms of rectangles, moreover, appear in the hierarchy as subclasses of GRect, which provides an intuitive illustration of the is-a relationship that defines subclassing.
The structure of the hierarchy, however, is not an open-and-shut case. The OOPS and ObjectDraw submissions, for example, include several intermediate classes and interfaces to ensure that the object classes offer only the methods that are appropriate to that class. Calls to setFilled on a GImage or setSize on a GString, for example, do not have obvious intuitive meanings. A strict application of object-oriented methods would dictate that those methods should not exist in those classes and that the inheritance hierarchy be factored in such a way that only the appropriate methods are available. Organizing the hierarchy in this way leads to the inclusion of ovals and images under an abstract intermediate class like RectangularShape in OOPS or Rect in ObjectDraw. There are three problems with this approach, as follows:
- The resulting hierarchy can be counterintuitive, particular for novices who a struggling to understand the conceptual model of inheritance. It seems quite reasonable for a GRoundRect to be a subclass of GRect because a rounded rectangle is still conceptually a rectangle. On the other hand, having GOval be a subclass of GRect (or even of RectangularShape) violates that intuition because an oval is not a rectangle.
- The additional classes add extra baggage to the package structure, which reduces its accessibility to introductory students.
- A complete factorization by method, at least in Java, requires considerable duplication of code, given the lack of multiple inheritance. The OOPS package, for example, defines interfaces like Colorable, Rotatable, and Sizeable to mark those classes capable of responding to those methods. The interfaces, however, cannot specify the code, which is probably the same in all of the responding subclasses.
The alternative approach is to flatten the hierarchy and define methods in GObject even if some subclasses cannot meaningfully respond. In the current implementation of the acm.graphics package, calls to setFilled and setColor are simply ignored if the responding class does use that property to paint the object. If a method invocation might indicate a conceptual failure on the student’s part—such as calling setSize on a GString when the supported method for changing the size of a string is setFont—the implementation of setSize can be overridden to produce an informative error message that directs the student to the source of the problem.
The graphical object classes shown at the bottom of Figure 7-2 are not sufficient in themselves. In order to display a GObject on the screen, the student needs to add it to some sort of “canvas” that is part of the standard window system. That role is fulfilled by the GCanvas class, which is described in section 7.4. As a convenience for clients who are running Swing applications outside of the applet world, the acm.graphics package includes a GFrame class, which embeds a GCanvas inside a JFrame.
The last three classes in Figure 7-2 are described later in this document. The GCompound class and the associated GContainer interface make it possible to define one GObject as a collection of others. This facility is described in section 7.6 as part of a general discussion of extensibility. The GPen object provides a simple mechanism for constructing line drawings that adopts a conceptual model of a pen drawing on the canvas, as described in section 7.7.
7.3 The GObject class
The question of what methods graphical objects should support is an important design concern. The public methods available to the class GObject in the acm.graphics package appear in Figure 7-3. Most of the subclasses implement only these methods, usually through inheritance. The only subclass in the standard shape hierarchy that defines any significant additional methods is GPolygon, which is described in section 7.6.
The proposals received by the Java Task Force differ in certain respects, but all nonetheless share a similar underlying model. In each of these designs, the student creates pictures by instantiating various graphical objects, installing them (sometimes implicitly by including the canvas as a parameter to the constructor) on a canvas of some sort, and then manipulating the display by sending messages to the objects to change their state and appearance.
Figure 7-3. Methods common to all graphical objects
Abstract method to paint the object | | |
void paint(Graphics g)
Paints the object using the graphics context g. All subclasses must implement this method. |
|
Methods to set and retrieve the position and size of the object | | |
void setLocation(double x, double y) or setLocation(Point pt)
Sets the location of this object to the specified point. |
void setSize(double width, double height) or setSize(Dimension size)
Changes the size of this object to the specified width and height. |
void translate(double dx, double dy)
Moves the object using the displacements dx and dy. |
void scale(double sx, double sy) or scale(double sf)
Changes the size of the object by the specified scale factor(s). |
double getX()
Returns the x-coordinate of the object. |
double getY()
Returns the y-coordinate of the object. |
double getWidth()
Returns the width of the object. |
double getHeight()
Returns the height of the object. |
Point getLocation()
Returns the location of this object as a Point with the components rounded to integers. |
Dimension getSize()
Returns the size of this object as a Dimension with the components rounded to integers. |
Rectangle getBounds()
Returns the bounding box of this object (the smallest rectangle that covers the figure). |
boolean contains(double x, double y) or contains(Point pt)
Checks to see whether a point is inside the object. |
|
Methods to set and retrieve visual properties of the object | | |
void setColor(Color c) and Color getColor()
Sets (or retrieves) the color used to display this object. |
void setFillColor(Color c) and Color getFillColor()
Sets (or retrieves) the color used to fill this object, which defaults to the object color |
void setFilled(boolean fill) and boolean isFilled()
Sets (or tests) whether this object is filled (true means filled, false means outlined). |
void setVisible(boolean visible) and boolean isVisible()
Sets (or tests) whether this object is visible. |
|
Methods that define this object’s relationship to its environment | | |
abstract void paint(Graphics g)
Paints the object using the graphics context g. All subclasses must implement this method. |
GContainer getParent()
Returns the parent of this object, which is the container in which it is enclosed. |
void moveToFront()
Moves this object to the front of its container where it may obscure objects in back. |
void moveToBack()
Moves this object to the back of its container where it may be obscured by objects in front. |
|
Methods to allow objects to respond to mouse events | | |
void addMouseListener(MouseListener listener)
Specifies a listener to process mouse events for this graphical object. |
void removeMouseListener(MouseListener listener)
Removes the specified mouse listener from this graphical object. |
void addMouseMotionListener(MouseMotionListener listener)
Specifies a listener to process mouse motion events for this graphical object. |
void removeMouseMotionListener(MouseMotionListener listener)
Removes the specified mouse motion listener from this graphical object. |
|
|
A comparison of the methods available to graphical objects in the various models appears in Figure 7-4. One of the most important differences is that the acm.graphics package allows graphical objects to field mouse events in exactly the same way that components do. That mechanism, and the rationale behind it, are discussed in section 7.5. The following notes offer a bit of background on the reasons for other changes:
Figure 7-4. Comparison of features provided in the submissions
| | ObjectDraw
[Bruce04a] | OOPS
[SandersK04a] | Stanford Graphics
[Parlante04a] | |
Checking containment
|
Setting fill
|
Setting fill color
|
Setting visibility
|
Supports general polygons
|
Changing z-ordering
|
Supports mouse interaction
|
Other features
|
|
|
|
yes
|
yes
|
no
|
fill is fixed for class
FramedRect/FilledRect |
yes
|
no
|
|
no
|
yes
|
no
|
yes, but uses deprecated
names show and hide |
yes, but uses deprecated
names show and hide |
no
|
yes, but you can’t find
out what the z-order is |
no
|
no
|
|
no
|
no
|
no
|
yes, but only in
the JDK 1.0 style |
yes, but only in
the JDK 1.0 style |
click-to-proceed only
|
overlaps method
|
supports rotation
can set frame thickness |
inset method
all objects are nestable |
| |
- Method naming. The method names used in all acm.graphics classes follow as closely as possible the patterns for method naming used in modern releases of the JDK. Particularly problematic are method names that have been deprecated for the Component class, such as show and hide, which have been replaced by setVisible and isVisible. Similarly, all mutator and accessor methods follow the Java Bean convention of using the set and get prefixes (plus is for booleans). More generally, whenever there is already a name in the AWT for the functionality provided by this package, it seems appropriate to use that name, as in the use of translate to express motion in terms of displacements from the current position.
- Filling. The model for filling an object differs in the various submissions. The minimalist Stanford Graphics proposal ignores the issue entirely: all shapes are filled. OOPS uses a model similar to the one proposed here in which students can turn filling off for individual objects; it also provides methods to set the fill color independently from that of the frame, which has been adopted for acm.graphics. ObjectDraw provides two parallel sets of classes, one filled and one framed. This seems unnecessarily complicated (and is probably a case in which to apply Occam’s Razor in its classic form, which warns that “entities should not be multiplied beyond necessity”).
- Z-ordering. Both ObjectDraw and the acm.graphics proposal provide some control over the stacking order in which the objects are placed on the canvas. The ObjectDraw model is in one respect more powerful, given that it supports sendForward and sendBackward in addition to sendToBack and sendToFront. To make z-ordering useful as a general tool, however, there must be some way to determine where an object falls within that order—information that appears to be unavailable in ObjectDraw. The acm.graphics design allows clients to iterate through the objects within a canvas, making it possible to determine where each object fits. Having this information available reduces the need for sendForward and sendBackward.
The last line in Figure 7-4 lists features that were part of one of the proposals but were not included in the acm.graphics package design, as follows:
- ObjectDraw allows an object to determine whether its space overlaps that of another through the inclusion of an overlaps method. This method would be straightforward to add, but the functionality is easily obtainable by calling intersects—which would be a more Java-compatible name—on the bounding rectangles.
- The ability to rotate arbitrary objects as in OOPS would be useful, but it depends on using Graphics2D for its internal operation. Using the Graphics2D interface instead of the more primitive Graphics interface has two downsides. First, writing code that uses it becomes more difficult, particularly in terms of its mathematical sophistication. That fact makes it unlikely that students would be able to write their own shape classes. Second, many browsers supply graphics contexts that don’t implement Graphics2D, which limits the range of platforms on which such code can run. In the acm.graphics design, only the GPolygon class supports rotation, where it can be implemented without recourse to Graphics2D. The capability of changing the size of the frame seems to move the package away from the model provided by java.awt.Graphics and does not appear to generate benefits that are worth that cost.
- The Stanford Graphics proposal includes an inset(dx, dy) method that shrinks an object by the specified displacements along each edge. This method is therefore analogous to—but opposite in direction from—the grow method in Rectangle (suggesting at a minimum that it be replaced by one with a more standard name). The underlying function, however, seems of minor utility and can easily be achieved by calling
| |
gobj.setBounds(gobj.getBounds().grow(-dx, -dy));
|
|
That proposal also makes every graphical object capable of containing other graphical objects. The notion of containment seems defensible as an idea, but not in such an undisciplined way, as outlined in section 7.6.
7.4 The GCanvas class
The GCanvas class provides the link between the world of graphical objects and the Java windowing system. Conceptually, the GCanvas class acts as a container for graphical objects and allows clients of the package to add and remove elements of type GObject from an internal display list. When the GCanvas is repainted, it forwards paint messages to each of the graphical objects it contains. Metaphorically, the GCanvas class acts as the background for a collage in which the student, acting in the role of the artist, positions shapes of various colors, sizes, and styles.
The methods supported by the implementation of the GCanvas class in the acm.graphics package are shown in Figure 7-5.
Figure 7-5. Public methods in the GCanvas class
Constructor | | |
GCanvas()
Creates a new GCanvas that contains no objects. |
|
Methods to add and remove graphical elements from a canvas | | |
void add(GObject gobj)
Adds a graphical object to the canvas without changing its location. |
void add(GObject gobj, double x, double y) or add(GObject gobj, Point pt)
Adds a graphical object to the canvas and sets its location to the specified point. |
void remove(GObject gobj)
Removes the specified graphical object from the canvas. |
void removeAll()
Removes all graphical objects and AWT components from the canvas. |
|
Methods to add and remove AWT components from the canvas | | |
void add(Component comp)
Adds an AWT component to the canvas, where it floats above the graphical elements. |
void add(Component comp, double x, double y) or add(Component comp, Point pt)
Adds an AWT component to the canvas and sets its location to the specified point. |
remove(Component comp)
Removes the specified component from the canvas. |
|
Methods to determine the contents of the canvas | | |
Iterator iterator()
Returns an iterator that runs through the graphical elements from back to front. |
Iterator iterator(int direction)
Returns an iterator that runs in the specified direction (BACK_TO_FRONT or FRONT_TO_BACK). |
int getElementCount()
Returns the number of graphical objects contained on the canvas. |
GObject getElement(int i)
Returns the graphical object at the specified index, numbering from back to front. |
|
Methods to support mouse interaction via subclassing | | |
GObject getElementAt(double x, double y) or getElementAt(Point pt)
Returns the topmost object containing the specified point, or null if no such object exists. |
void onMouseClicked(double x, double y)
Invoked whenever a mouse click occurs in the canvas. |
void onMousePressed(double x, double y)
Invoked whenever the mouse button is pressed in the canvas. |
void onMouseReleased(double x, double y)
Invoked whenever the mouse button is released in the canvas. |
void onMouseMoved(double x, double y)
Invoked whenever the mouse button is moved in the canvas. |
void onMouseDragged(double x, double y)
Invoked whenever the mouse button is dragged (moved with the button down) in the canvas. |
|
Methods to control repaint efficiency (not likely to be used by novices) | | |
void setAutoRepaintEnabled(boolean state)
Determines whether repaint requests occur automatically when a graphical object changes. |
boolean isAutoRepaintEnabled()
Returns whether automatic repainting is enabled. |
|
|
Adding and removing objects from a canvas
The first set of methods in Figure 7-5 seems straightforward given the fact that a GCanvas is conceptually a container for GObject values. The container metaphor suggests the functionality provided by the add, remove, removeAll methods in Figure 7-5, which are analogous in their behavior to the identically named methods in Container.
| I have to admit I’m baffled by the decision to bind graphical objects to their canvas at instantiation time. I’d love to hear the reasons behind that design. |
Interestingly, none of the three submitted proposals chose to implement the relationship between graphical objects and their canvases using this metaphor of adding objects to a container. In each of the packages, the container is specified—implicitly in the case of OOPS—at the time the graphical object is constructed. Such an design seems less than ideal for three reasons. First, the strategy runs counter to the model provided by components and containers and will therefore provide no help when the student moves on AWT and Swing. Second, such a restriction seems to violate the intuitive notion of a collage, in which one creates freestanding objects and then pastes them on a canvas. Third, you often need to have the object to know where to put it in the container, as illustrated by the following code, which centers a GObject object in the GCanvas named gc:
| |
GString gstr = new GString("Hello");
double x = (gc.getWidth() - gstr.getWidth()) / 2;
double y = (gc.getHeight() - gstr.getHeight()) / 2;
gc.add(gstr, x, y);
|
|
It’s not clear how you would put the object in the right place without being able to instantiate the freestanding object. The best you could do would be add it somewhere else (possibly invisibly, as in OOPS where one must call show before the object appears) and then move it to the center.
Adding and removing AWT components to a canvas
The next set of methods from Figure 7-5 provide analogous capabilities for adding and removing an AWT component (and therefore a JComponent or any of its subclasses) from a GCanvas. Students who have gotten into the habit of adding a GObject to a GCanvas will find it natural to add some other graphical object—a JButton perhaps—to a GCanvas as well. As an example, the call
| |
gc.add(new JButton("Test"), 75, 50);
|
|
produces a display such as the one shown on the right. The JButton is fully active and can accept listeners, just as it can in any other context.
Given that GCanvas extends Container, the simple versions of the add and remove methods already exist by inheritance, although it is useful to reimplement these methods slightly to give them more useful semantics. The first change is that GCanvas objects should use null as their default layout manager so that the positioning of the AWT objects is under client control, just as is true for graphical objects. Second, the add method must check the size of the component and set it to its preferred size if its bounds are empty. These simple changes seem to do exactly what students would want.
Determining the contents of a canvas
The third set of methods in Figure 7-5 make it possible for clients to figure out what graphical elements have been added to a GCanvas and provide a couple of approaches for doing so. The strategy that fits best with modern disciplines for using Java is to use an iterator that runs through the elements of a collection. The iterator provides that functionality in the conventional Java form, making it possible to write
| |
for (Iterator i = gc.iterator(); i.hasNext(); ) {
GObject gobj = (GObject) i.next();
. . . code for this element . . .
}
|
|
or, in Java 1.5, the abbreviated form
| |
for (GObject gobj : gc) {
. . . code for this element . . .
code
|
|
There are, however, some problems in adopting this strategy. First, there are two reasonable orders in which to process the elements of a GCanvas. If you are doing something analogous to painting, you want to go through the elements from back to front so that the elements at the front of the stacking order correctly obscure those behind them. On the other hand, if you are fielding mouse events, you want to go through the elements from front to back so that primacy on receiving the event goes to the graphical objects in front. (Both painting and mouse-event dispatching are provided by the package, so students need not actually code these two mechanisms, but might sometime want to do something similar.) To permit both strategies, the iterator method takes an optional argument that can be either BACK_TO_FRONT or FRONT_TO_BACK to specify the desired direction.
The second problem is that iterators are not supported on all platforms, since they were introduced in JDK 1.2. A large fraction of browsers continue to run only those applets compiled for JDK 1.1. To make it possible to use this package in applets that run on the maximum range of browsers, the methods getElementCount and getElement provide a lower-level mechanism for sequencing through the elements in any order.
7.5 Responding to mouse events
The evolutionary history of Java provides us with two strategies for responding to mouse events. The model that was defined for JDK 1.0 was based on callback methods whose behavior was defined through subclassing. Thus, to detect a mouse click on a component, you need to define a subclass that overrides the definition of mouseDown with a new implementation having the desired behavior. That model was abandoned in JDK 1.1 in favor of a new model based on event listeners. Under this paradigm, you add the necessary suite of methods to implement MouseListener to some class and then add some object of that class as a listener on the component whose events you want to catch. These models are quite different, and there is no obvious sense in which learning one helps prepare you to learn the other.
The two submitted packages that offer mouse support each provide a mechanism for responding to mouse events whose design is rooted in the JDK 1.0 model. The graphical object types in the OOPS proposal, for example, define methods for mousePressed, mouseReleased, mouseClicked, and mouseDragged (but not, interestingly, mouseMoved mouseEntered, or mouseExited) that are invoked whenever the specified event is detected over that object. In ObjectDraw, event handling takes place at the level of the canvas (in the class AWTWindowController) rather than the object and is provided by cascading pairs of callback methods. The mousePressed method, for example, is called in exactly the same way as it is in OOPS and allows clients to override the behavior at a level with access to the actual MouseEvent structure. To shield novices from that complexity, however, the default behavior of mousePressed is to invoke onMousePressed, passing in the point as a compound Location object that encapsulates the double-valued coordinates. Thus, novices can override this method instead if all they need are the mouse coordinates.
It is important to note that each of these approaches requires subclassing to intercept the event. In some sense, the biggest change in discipline between the JDK 1.0 and 1.1 event models is the elimination of the need for subclassing in the new paradigm. If you want to put a JButton up in a window, you don’t subclass JButton to give it new behavior. You simply construct one and then add listeners to some other object.
It may well be that novices would find it easier to work with the JDK 1.0 strategy, particularly if our library classes hide the event structures, as they do in ObjectDraw. At the same time, many potential adopters would look askance at a package that seems like a throwback to a long-obsolete version of Java. While there may be good reasons to supply such an interaction mechanism for teachers who would appreciate its relative simplicity (and who might actually view the need for subclassing as a feature in the sense that it forces students to understand that model), it must be possible to use the ACM graphics package in a manner consistent with a more modern coding style.
It is, of course, possible to do so under any of these packages simply by adding a new listener to whatever class plays the role of the canvas and fielding the events from there. The difficulty, however, is that the most intuitive model for event handling—and the one that corresponds to the behavior of the AWT hierarchy—would have the graphical objects be the source for the events rather than the canvas in which those objects are contained. To illustrate the distinction, it is useful to consider how one might use the mouseEntered and mouseExited methods in a canvas-based listener. Although one can construct situations in which you need to notice that the mouse has entered the canvas, what most students are likely to want is some way of detecting when the mouse has entered one of their objects. Such a capability enables the simulation of roll-over buttons, which students seem to enjoy.
To support that style of interaction, the acm.graphics enables mouse event listening for the GObject class. As an illustration of this behavior, the methods
| |
public void mouseEntered(MouseEvent e) {
((GObject) e.getSource()).setColor(Color.red);
}
public void mouseExited(MouseEvent e) {
((GObject) e.getSource()).setColor(Color.black);
}
|
|
define listener methods that implement rollover behavior for any GObject that adds a mouse listener containing this code. Moving the mouse into the containment region of the object turns the object red; moving the mouse out again turns it black.
Figure 7-6 provides a more extensive example of the use of mouse events in objects by presenting the complete code for an application that installs two shapes—a red rectangle and a green oval—and allows the user to drag either shape using the mouse. The program also illustrates z-ordering by moving the current object to the front on a mouse click. This example is running in the following applet, so you can try it out yourself:
Figure 7-6. Program to illustrate mouse dragging in a GFrame application
/* File: ObjectDragExample.java */
import java.awt.*;
import java.awt.event.*;
import acm.graphics.*;
/** This class displays a mouse-draggable rectangle and oval */
public class ObjectDragExample extends GFrame
implements MouseListener, MouseMotionListener {
/** Initializes and installs the objects in the GFrame */
public ObjectDragExample() {
setBounds(10, 40, 500, 300);
GRect rect = new GRect(100, 100, 150, 100);
rect.setFilled(true);
rect.setColor(Color.red);
rect.addMouseListener(this);
rect.addMouseMotionListener(this);
add(rect);
GOval oval = new GOval(300, 115, 100, 70);
oval.setFilled(true);
oval.setColor(Color.green);
oval.addMouseListener(this);
oval.addMouseMotionListener(this);
add(oval);
show();
}
/** Called on mouse press to record the coordinates of the click */
public void mousePressed(MouseEvent e) {
last = e.getPoint();
}
/** Called on mouse drag to move the object generating the event */
public void mouseDragged(MouseEvent e) {
GObject gobj = (GObject) e.getSource();
Point pt = e.getPoint();
gobj.translate(pt.x - last.x, pt.y - last.y);
last = e.getPoint();
}
/** Called on mouse click to move this object to the front */
public void mouseClicked(MouseEvent e) {
((GObject) e.getSource()).moveToFront();
}
public void mouseReleased(MouseEvent e) { }
public void mouseEntered(MouseEvent e) { }
public void mouseExited(MouseEvent e) { }
public void mouseMoved(MouseEvent e) { }
/** Standard entry point for the application */
public static void main(String[] args) {
new ObjectDragExample();
}
/** Private data field used to record the last mouse click */
private Point last;
} |
7.6 Extensibility
With only 15 classes and interfaces, the acm.graphics package is small enough for teachers and students to understand the whole of the design in a relatively short amount of time. Despite its modest size, however, the facilities provided by the package enable students to construct extremely sophisticated designs. For simple applications, the classes provided by the package are sufficient. As applications become larger and more complex, clients of the acm.graphics package will find it useful to extend the basic functionality by defining new classes that build on the existing ones. The next few subsections describe four strategies for extending the predefined object hierarchy, as follows:
- Extending the existing shape classes
- Extending the GPolygon class
- Creating compound objects using GCompound
- Deriving subclasses directly from GObject
Extending the existing shape classes
The simplest form of extension available to students is creating subclasses of the existing shapes. Such subclasses are useful, for example, in those applications in which you need to create many shapes that share a common property. Such properties can be set in the subclass constructor, thereby freeing you from the need to set them for each individual object. Consider, for example, the following pair of classes:
| |
class GFilledSquare extends GRect {
public GFilledSquare(double x, double y, double size) {
super(x, y, size, size);
setFilled(true);
}
}
class GRedSquare extends GFilledSquare {
public GRedSquare(double x, double y, double size) {
super(x, y, size);
setColor(Color.red);
}
}
|
|
In this example, the class GFilledSquare represents a rectangle object that is initially square (in the sense that only a single dimension is required for both width and height) and filled; GRedSquare further extends that class to create a filled square that is initially red. Given that these classes inherit all the methods of GRect (and from there the methods of GObject), you can change any of these properties later.
This simple style of extension is certainly accessible to most introductory students and gets them using the notions of subclassing and inheritance early. Its flexibility, however, is limited by the need to find an existing class whose paint method draws the desired figure.
Extending the GPolygon class
As it turns out, the extension style that has proven to be most useful in practice consists of defining new subclasses of GPolygon, which was described in only a cursory way in section 7.3. Unlike the other shape classes, a GPolygon object is not completely defined through the act of calling its constructor. The constructor for this class creates an empty polygon, to which the client must then add edges. The following code offers an illustration of the process of creating a GPolygon by creating a square whose origin (i.e., the location of the GPolygon object itself) is at the center of the figure:
| |
GPolygon createSquare(double side) {
GPolygon square = new GPolygon();
square.startPolygon(-side / 2, -side / 2);
square.addEdge(side, 0);
square.addEdge(0, side);
square.addEdge(-side, 0);
square.addEdge(0, -side);
square.endPolygon();
return square;
}
|
|
The startPolygon method establishes the starting point of the polygon relative to the origin of the figure, which need not be on the polygon boundary (and usually isn’t). The addEdge method adds an edge from the current point and is used to build up the polygonal outline. The endPolygon method closes the figure and makes it available for display.
For many polygonal figures, it is easier to express edges in polar coordinates, which is supported in the GPolygon class by the method addEdgeInPolarCoordinates, which is identical to addEdge except that its arguments are the length of the vector and a direction expressed in degrees counterclockwise from the +x axis. This method makes it easy to create more interesting figures, such as the centered hexagon generated by the following method:
| |
GPolygon createHexagon(double side) {
GPolygon hex = new GPolygon();
hex.startPolygon(-side, 0);
int angle = 60;
for (int i = 0; i < 6; i++) {
hex.addEdgeInPolarCoordinates(side, angle);
angle -= 60;
}
hex.endPolygon();
return hex;
}
|
|
As with any of the other shape classes, a GPolygon can be filled or outlined, given a color, and manipulated by standard GObject methods such as setLocation, translate, and scale. In addition, the GPolygon class supports rotate, which rotates the polygon around its origin by a specified angle.

The square and hexagon examples each create a new GPolygon object that draws the desired figure. The GPolygon class can also be used as the base class for new shape classes whose outline is a polygonal region. This technique is illustrated by the GStar class in Figure 7-7, which draws the five-pointed star shown on the right. The only complicated part of the class definition is the geometry required to compute the coordinates of the starting point of the figure, but these calculations are made a little easier by the inclusion of static methods in the GPolygon class that compute trigonometric functions in degrees (a list of those functions appears in Figure 7-10 as part of the discussion of the GPen class, which also supplies these methods). This code also illustrates the useful strategy of constructing the figure inside a unit square and then scaling it to the appropriate dimensions.
Figure 7-7. Class definition for a five-pointed star
/** Defines a graphical object that appears as a five-pointed star */
public class GStar extends GPolygon {
/** Constructs a star centered in a square of the specified size */
public GStar(double size) {
double sinTheta = sinD(18);
double b = 0.5 * sinTheta / (1.0 + sinTheta);
double edge = 0.5 - b;
startPolygon(-0.5, -b);
int angle = 0;
for (int i = 0; i < 5; i++) {
addEdgeInPolarCoordinates(edge, angle);
addEdgeInPolarCoordinates(edge, angle + 72);
angle -= 72;
}
endPolygon();
scale(size);
}
/** Constructs a star centered at (x, y) */
public GStar(double x, double y, double size) {
this(size);
setLocation(x, y);
}
} |
Creating compound objects using GCompound
| Kim and Scott have each raised questions about including a compound class. I’ve attempted to make the case here. I find that I use them quite often as I build demo programs for the graphics packag |
Although the GPolygon class is useful in a variety of contexts, it is limited to those applications in which the desired graphical object can be described as a simple closed polygon. Many graphical objects that one might want to define don’t fit this model. Given that the predefined shape classes are precisely aligned with the drawing capabilities available in the AWT Graphics class, anything that one could draw using the traditional Java paradigm can be described as a collection of shapes from the predefined set. If it were possible, therefore, to define new graphical objects as aggregates of existing ones, the resulting mechanism would enable clients of the graphics package to encapsulate any graphical figure as a single graphical object.
This fact provides the motivation behind the inclusion of the GCompound class, in the acm.graphics package. The methods available for GCompound are in some sense the union of those available to the GObject and GCanvas classes. As a GObject, a GCompound responds to method calls like setLocation and scale; as an implementer (like GCanvas) of the GContainer interface, it supports methods like add and remove. The usual paradigm for using a GCompound is to create an empty one and then add other graphical objects to it using coordinates relative to the origin of the compound object rather than to the canvas in which the compound will eventually be enclosed. You can then add the compound object to the canvas and move all of its elements as a unit.
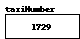 A practical application of the use of GCompound is illustrated by the code in Figure 7-8. The idea behind the GVariable class is to create a new graphical object that represents a traditional box diagram of a variable, such as the one shown at the right. In terms of its graphical representation, the GVariable has three components: a GRect that displays the box, a GString to display the variable name, and another GString representing the value. To the client, however, the GVariable offers a more conceptual interface that supports setting and retrieving the value of the variable, represented as an arbitrary object. The box diagram shown, for example, might be generated by the following statements:
A practical application of the use of GCompound is illustrated by the code in Figure 7-8. The idea behind the GVariable class is to create a new graphical object that represents a traditional box diagram of a variable, such as the one shown at the right. In terms of its graphical representation, the GVariable has three components: a GRect that displays the box, a GString to display the variable name, and another GString representing the value. To the client, however, the GVariable offers a more conceptual interface that supports setting and retrieving the value of the variable, represented as an arbitrary object. The box diagram shown, for example, might be generated by the following statements:
| |
GVariable taxiNumber = new GVariable("taxiNumber");
taxiNumber.setValue(new Integer(1729));
|
|
Figure 7-8. The GVariable class implementing using GCompound
/* Class: GVariable */
/**
* This class represents a labeled box with contents that can be
* set and retrieved by the client. It is intended for displaying
* the value of a variable.
*/
class GVariable extends GCompound {
public static final double VARIABLE_WIDTH = 75;
public static final double VARIABLE_HEIGHT = 25;
public static final Font FONT = new Font("Monospaced",
Font.BOLD, 10);
/** Constructs a GVariable object with the specified name. */
public GVariable(String name) {
GRect box = new GRect(VARIABLE_WIDTH, VARIABLE_HEIGHT);
box.setFilled(true);
box.setFillColor(Color.white);
add(box, 0, 0);
GString label = new GString(name);
label.setFont(FONT);
add(label, 0, -label.getDescent() - 1);
display = new GString("");
display.setFont(FONT);
add(display);
centerDisplay();
}
/** Sets the value of the variable. */
public void setValue(Object value) {
this.value = value;
display.setString(value.toString());
centerDisplay();
}
/** Returns the value of the variable. */
public Object getValue() {
return value;
}
/** Centers the value string in the variable box. */
private void centerDisplay() {
double x = (VARIABLE_WIDTH - display.getWidth()) / 2;
double y = (VARIABLE_HEIGHT + display.getAscent()) / 2;
display.setLocation(x, y);
}
/* Private state */
private GString label, display;
private Object value;
} |
The question of whether to include GCompound in the acm.graphics package prompted considerable discussion within the Java Task Force. The arguments against including are predicated largely on the principle of minimizing complexity: all other things being equal, it’s best to define as few classes as possible to achieve the desired goal of producing a usable object-based graphics package. The GCompound class, by definition, provides no new capabilities in terms of what clients of the package can draw on the screen. The arguments in favor include the following:
- The GCompound class provides a powerful abstraction mechanism for creating new objects that maintain their conceptual integrity.
- GCompound serves as the base class for a wide spectrum of useful classes that many adopters might want to use, such as the GVariable class used in the example. The online tutorial supplied with the ACM libraries uses many of these.
- The inclusion of this class and the associate GContainer interface make it possible for teachers to use the acm.graphics package as a paradigmatic example of containment as well as subclassing. The understanding that students gain through this process will help them understand the relationship between the Component and Container classes in the AWT, which is directly parallel to this design. A Container is a Component that also contains Components, just as a GCompound is a GObject that also contains GObjects.
- It is not really possible to add the GCompound class as an independent extension because the design of the rest of the package depends to a certain extent on whether the GCompound class exists. If there were no GCompound class, for example, there would be no obvious need for the GContainer interface, even though that interface is integral to a clean design of the compound object facility. The only possible parent for a GObject would be the GCanvas in which it resides, and it would be difficult to explain the existence of the GContainer interface except as a gateway to future extensions “left to the reader as an exercise.” Such a package would appear unfinished.
- There are many aspects of the design and implementation of GCompound that are hard to get right, and it seems dangerous to have such a useful facility implemented independently by individual adopters of the package. In particular, handling mouse events that occur in the region of a compound object requires some subtlety to retain consistent semantics.
Deriving subclasses directly from GObject
The strategies presented earlier all have the advantage—particularly for novices—that they allow subclass designers to remain entirely in the acm.graphics world, without exposing the implementation structures underneath. It is also possible to extend GObject directly. In this case, however, the subclass must provide a definition of the method
| |
public abstract void paint(Graphics g);
|
|
which means that whoever writes that subclass has to understand the java.awt.Graphics class and its methods. That said, it turns out to be relatively straightforward to write such classes, and we should certainly expect teachers and more advanced students to do so.
To offer at least one example of how such extensions might work, the code in Figure 7-9 reimplements the GVariable example from the preceding section as a direct subclass of GObject. Much of the code is the same. The difference is that the painting of the object (including the centering of the value string) is now supplied by an explicit paint method. For Java programmers, the resulting code is not too difficult. The class definition still fits on one page, and the implementation of paint is reasonably straightforward. For a novice, however, this implementation requires coming to understand several new AWT concepts, including the classes Graphics and FontMetrics. The earlier implementation based on GCompound hides all these implementation details.
Figure 7-9. The GVariable class implemented as a direct GObject subclass
/* Class: GVariable */
/**
* This class represents a labeled box with contents that can be
* set and retrieved by the client. It is intended for displaying
* the value of a variable.
*/
class GVariable extends GObject {
public static final double VARIABLE_WIDTH = 75;
public static final double VARIABLE_HEIGHT = 25;
public static final Font FONT = new Font("Monospaced",
Font.BOLD, 10);
/** Constructs a GVariable object with the specified name. */
public GVariable(String name) {
setSize(VARIABLE_WIDTH, VARIABLE_HEIGHT);
this.name = name;
value = null;
}
/** Sets the value of the variable. */
public void setValue(Object value) {
this.value = value;
repaint();
}
/** Returns the value of the variable. */
public Object getValue() {
return value;
}
/** Draws the object using the graphics context g. */
public void paint(Graphics g) {
Rectangle r = super.getBounds();
g.setColor(Color.white);
g.fillRect(r.x, r.y, r.width, r.height);
g.setColor(getColor());
g.drawRect(r.x, r.y, r.width, r.height);
g.setFont(FONT);
FontMetrics fm = g.getFontMetrics();
g.drawString(name, r.x, r.y - fm.getDescent() - 1);
String str = (value == null) ? "" : value.toString();
int x = r.x + (r.width - fm.stringWidth(str)) / 2;
int y = r.y + (r.height + fm.getAscent()) / 2;
g.drawString(str, x, y);
}
/* Private state */
private String name;
private Object value;
} |
Managing extensions
The existence of any strategy for defining new GObject subclasses, whether or not a GCompound class exists, invites adopters of the package to create new classes, some of which will undoubtedly be of interest to the broader community. One of the lessons of the extensible language movements of the 1970s—and indeed one of the underlying reasons for the success of very rich software development environments like the JDK—is that programmers are generally less concerned with extensibility than they are with extensions. Being able to build your own extensions is of interest to some; picking up extensions that someone else has developed is of great interest to a much broader spectrum of users. It therefore seems reasonable to expect that educators (and possibly others) who adopt the acm.graphics package will be willing both to supply new GObject classes to a common repository and to make use of ones that others put there.
Understanding how to manage such a repository needs to be part of the follow-on work envisioned by the Java Task Force. Presumably, it would make sense to establish some vetting process by which submissions could be evaluated and checked for consistency. Those that pass muster—and that come with a required set of materials including a javadoc description and source code distributable under some form of open source license—could then be put into a repository somewhere. Such a repository would increase community buy-in to the ACM libraries generally and make available an array of tools beyond anything that the task force itself could undertake to do.
At the same time, it seems important that the extended classes in the repository not become part of the acm.graphics package but remain as compatible supplements to it. Trying to manage a series of staged releases to accommodate new community-supplied classes seems like a fool’s errand and would reintroduce the instability that has plagued Java itself. As long as they stay within the 15 classes defined in the acm.graphics package, textbook authors and other resource developers can feel confident that the materials they develop will not quickly become dated. Similarly, teachers will not have to worry that the curricular materials they develop during one year might become obsolete in the next.
7.7 The GPen mechanism
| In many ways, it seems odd to include this class in the package, as opposed to offering it as one of the extensions available from the repository described in the preceding section. My reason for proposing it here as a full-fledged member of the package is that I expect it will be a particularly attractive feature for those who teach at the precollege level. Making it part of the package enables textbook authors to write about it and ensures that it is part of the stable framework of the acm.graphics package. |
The one remaining class to describe in the acm.graphics package is the GPen class, which doesn’t really fit into the other categories. At the implementation level, the GPen class is simply a graphical object capable of tracing a path and, equally importantly, of remembering the path it has drawn, thereby allowing it to support repainting. From the client’s point of view, GPen provides a simple approach for implementing the “turtle graphics” model described in Seymour Papert’s Mindstorms [Papert80]. The turtle graphics model has proven to be a useful pedagogical tool, particularly at the precollege level. The GPen class provides a standard framework for using turtle graphics within the acm.graphics package in a way that is consistent with the rest of the package design. Instructors who start students off drawing figures with a GPen object should be able to move smoothly to the other classes in the package.
The methods available in the GPen class (including a few key methods inherited from GObject) are shown in Figure 7-10. The most important of these are setLocation (or translate to specify relative motion) and drawLine. The former corresponds to picking up the pen and moving it to a new location; the latter represents motion with the pen against the canvas, thereby drawing a line. Each subsequent line begins where the last one ended, which provides the notion of a “current point” that is integral to the turtle graphics model.
Figure 7-10. Public methods in the GPen class
Constructors | | |
GPen()
Creates a new .GPen object with an empty path. |
GPen(double x, double y)
Creates a new .GPen object whose initial location is the point (x, y). |
|
Methods to reposition and draw lines with the pen | | |
void setLocation(double x, double y)
Moves the pen to the specified absolute location. |
void translate(double dx, double dy)
Moves the pen using the displacements dx and dy. |
void translateUsingPolarCoordinates(double r, double theta)
Moves the pen r pixel units in the direction theta, measured in degrees. |
void drawLine(double dx, double dy)
Draws a line with the specified displacements, leaving the pen at the end of that line. |
void drawLineUsingPolarCoordinates(double r, double theta)
Draws a line r pixel units in the direction theta, measured in degrees. |
void eraseAll()
Removes all lines from this pen’s path and repositions it at the origin. |
|
Methods to define a filled region bounded by pen strokes | | |
void startFilledRegion()
Fills the polygon formed by lines drawn between here and the next endFilledRegion. |
endFilledRegion()
Ends the filled region begun by startFilledRegion. |
|
Methods to control the appearance of the pen itself | | |
void setPenVisible(boolean visible)
Sets whether the pen itself is visible, as opposed to its track. This setting is normally false. |
boolean isPenVisible()
Returns true if the pen is visible, and false otherwise. |
void setPenImage(Image image)
Sets an image to display the pen (such as a turtle). By default, the pen appears as a quill. |
Image getPenImage()
Returns the image currently used to display the pen. |
void setPenDelay(double delayTime)
Waits for the specified delay time (measured in milliseconds) between each pen action. |
double getPenDelay()
Returns the pen delay last set by setPenDelay. |
|
Static methods to support degree-based trigonometric calculations | | |
double sinD(double angle)
Returns the trigonometric sine of an angle measured in degrees. |
double cosD(double angle)
Returns the trigonometric cosine of an angle measured in degrees. |
double tanD(double angle)
Returns the trigonometric tangent of an angle measured in degrees. |
double toDegrees(double radians)
Converts an angle from radians to degrees. |
double toRadians(double degrees)
Converts an angle from degrees to radians. |
double distance(double x, double y)
Returns the distance from the origin to the point (x, y). |
double distance(double x0, double y0, double x1, double y1)
Returns the distance between the points (x0, y0) and (x1, y1). |
double angle(double x, double y)
Returns the angle between the origin and the point (x, y), measured in degrees. |
|
|
The turtle graphics model seems to provide the only straightforward way to code a variety of recursive figures, such as the Koch fractal (“snowflake” curve) or the Sierpinski triangle. The following code, for example, draws a Koch fractal of the indicated order and size (horizontal extent) with its geometric center at the point (x, y):
| |
void drawKochFractal(double x, double y, double size, int order) {
GPen pen = new GPen(x, y);
pen.translate(-size / 2, -size / (2 * Math.sqrt(3)));
drawFractalLine(pen, size, 0, order);
drawFractalLine(pen, size, -120, order);
drawFractalLine(pen, size, +120, order);
}
void drawFractalLine(GPen pen, double len, int theta, int order) {
if (order == 0) {
pen.drawLineUsingPolarCoordinates(len, theta);
} else {
drawFractalLine(pen, len / 3, theta, order - 1);
drawFractalLine(pen, len / 3, theta + 60, order - 1);
drawFractalLine(pen, len / 3, theta - 60, order - 1);
drawFractalLine(pen, len / 3, theta, order - 1);
}
}
|
|
Calling drawKochFractal(cx, cy, 100, 3) (where cx and cy are the coordinates of the center of the figure) generates the following picture:
The following applet draws the Koch fractal, allowing the user to set a variety of parameters:



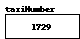 A practical application of the use of GCompound is illustrated by the code in Figure 7-8. The idea behind the GVariable class is to create a new graphical object that represents a traditional box diagram of a variable, such as the one shown at the right. In terms of its graphical representation, the GVariable has three components: a GRect that displays the box, a GString to display the variable name, and another GString representing the value. To the client, however, the GVariable offers a more conceptual interface that supports setting and retrieving the value of the variable, represented as an arbitrary object. The box diagram shown, for example, might be generated by the following statements:
A practical application of the use of GCompound is illustrated by the code in Figure 7-8. The idea behind the GVariable class is to create a new graphical object that represents a traditional box diagram of a variable, such as the one shown at the right. In terms of its graphical representation, the GVariable has three components: a GRect that displays the box, a GString to display the variable name, and another GString representing the value. To the client, however, the GVariable offers a more conceptual interface that supports setting and retrieving the value of the variable, represented as an arbitrary object. The box diagram shown, for example, might be generated by the following statements:
