Variations on the Game of Life

HighLife

HighLife is a variant of Conway's Game of Life with one additional rule: a dead cell comes to life if it is surrounded by 6 living cells. While many patterns function similarly in both Life and HighLife, HighLife is best known for the "replicator" pattern, which actually makes copies of itself (an equivalent pattern has not been found in the standard Game of Life).

A replicator in the HighLife variant of Life.

3D Life

Although 2-dimensional cellular automata are the most well-known, 3D variants are also possible to simulate. Some rulesets result in static patterns and gliders analogous to those found in Conway's original 2-dimensional version. Here is a page with some interesting observations about 3D variants of the Game of Life.

1-Dimensional Cellular Automata

Cellular automata are also possible to construct in a 1-dimensional space. These types of automata are generally drawn in two dimensions, with the Y axis corresponding to successive generations.

Rule 30, a 1-dimensional cellular automata developed by Stephen Wolfram, is particularly interesting because it produces chaotic and complex patterns from simple rules.

A sample of the results generated from a single initial cell by using Rule 30.

Rule 90, another 1-dimensional cellular automaton, generates a Sierpinksi Triangle pattern when seeded with a single live cell.

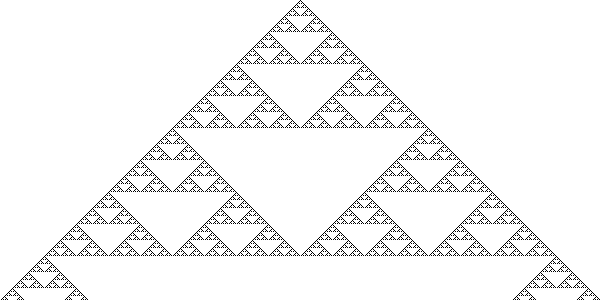Sierpinski Triangle

Non-Square Grid Shapes

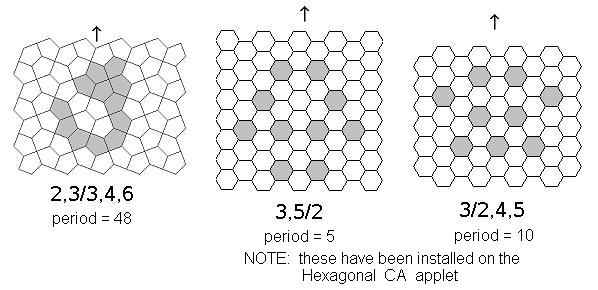Gliders in Pentagonal and Hexagonal variations of Life.

Although they have not been studied extensively, Triangular, Pentagonal, and Hexagonal versions of Life have been implemented, replacing the square grid with other tilings and affecting the number of neighbors that each cell has.

Multiple Colors

Another class of variations on the standard Game of Life is cellular automata involving more than 2 possible colors or states for each cell.

The Immigration Game

The Immigration Game is identical to the original Game of Life, except any newborn cell is colored according to the majority color of its 3 living neighbors. Although the patterns generated in the Immigration Game are no different than the ones in Conway's Game of Life, the colors can interact in interesting ways--including cyclic patterns.

The Rainbow Game of Life

The Rainbow Game of Life is similar to the Immigration Game, only newborn cells instead are colored based on the average color values of their parent cells. Thus, a cell which is born from two black cells and one white cell will have a dark gray appearance.

The Rainbow Game of Life is notable for being somewhat analogous to genetic properties spreading through a population of creatures. Some investigations on the propagation of colors in the Rainbow Game of Life can be seen here.

The Immigration Game and the Rainbow Game of Life can both be viewed and played here.

Cyclic Cellular Automata

In cyclic cellular automata, an ordering of multiple colors is established. Whenever a cell is neighbored by a cell whose color is next in the cycle, it copies that neighbor's color--otherwise, it remains unchanged.

One dimensional cyclic cellular automata can be used to model particles that undergo ballistic annihilation. Cycles involving more than 4 colors tend to produce patterns that stabilize more quickly when compared to 3 or 4-color cycles.

Two dimensional cyclic cellular automata typically result in spiraling patterns that eventually consume the entire grid. "Demon" artifacts, as shown below, create these spirals and are constructed from adjacent groups of cells which constantly devour each other and create a rotating pattern.

Wireworld

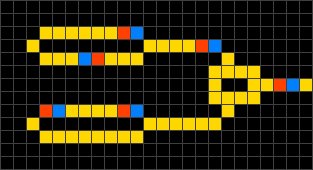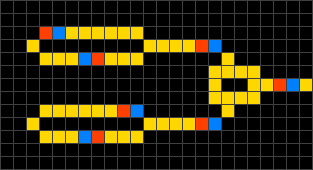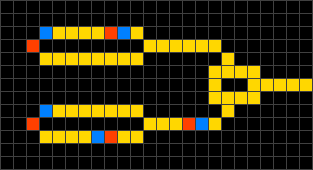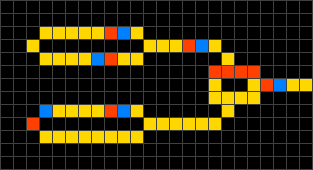Wireworld is a cellular automaton that simulates electronic devices and logic gates by having cells represent electrons traveling across conductors. Wireworld uses four possible cell states and has the following rules:
-Empty cells (black) always remain empty.
-Electron heads (blue) become electron tails in the succeeding generation.
-Electron tails (red) become conductors.
-Conductors (yellow) become electron heads if exactly one or two neighboring cells are electron heads. Otherwise, they remain as conductors.
Using these four simple rules, it is possible to design structures such as diodes (shown below), logic gates, and clock generators. Components are relatively easy to combine and the capabilities of the automaton make it Turing-complete. In fact, a computer that calculates prime numbers has been designed within the Wireworld system.

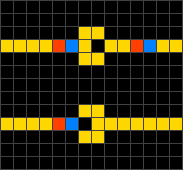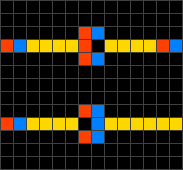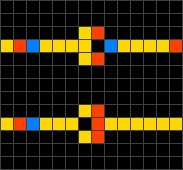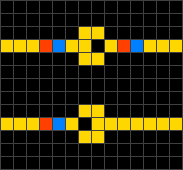Diodes in the Wireworld cellular automaton.

Mirek Wojtowicz's site on cellular automata contains information about even more variations on the Game of Life.

Timm[ie] Wong, September 2008