
The Maximal Clique Problem
Although many theoretical papers have been published on DNA computing since Adleman’s first crude demonstration in 1994, it would be over two years, in 1997, until another NP complete problem would be solved. This problem was the Maximal Clique Problem: given a group of vertices some of which have edges in between them, the maximal clique is the largest subset of vertices in which each point is directly connected to every other vertex in the subset. Every time a new point is added, the number of total cliques that must be searched at least doubles; hence we have an exponentially growing problem. Once again, researches sought to take advantage of DNA’s high level parallelism which would essentially allow all the possible paths to be calculated simultaneously. After all the possible cliques were constructed, the scientists would simply need to fish out the largest clique. However, like many DNA experiments, each possible “choice” needed a unique DNA strand. This is a problem because, as noted early, the number of cliques grows exponentially. In Adleman’s experiment, each city and every connecting path had to be “hardcoded,” in other words, specially made to order in a biology lab. In a problem with more cities, it would be virtually impossible to manually create every possible path. Ouyang and company designed an algorithm that would only require the manual creation a linearly growing number of DNA strands, 2N to be exact, where ‘N’ is the number of vertices in the graph.

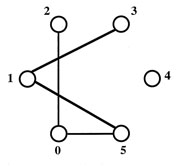
The six-node graph for this problem
The maximum clique size is 4, and the maximum clique contains the nodes
2,3,4,5.
Their algorithm went like this. Each possible clique was represented by a binary number of N bits where each bit in the number represented a particular vertex. If a certain bit held a ‘1’, the corresponding vertex was in the clique, if it was a ‘0’, it wasn’t part of the clique. For example, a clique containing the first four nodes would be “001111”.
 Then, they removed
those cliques that contained illegal connections, because not every node
was interconnected in the original graph (otherwise the entire graph would
be one big clique). The figure on the right shows the illegal paths. For
example, any strand with a "1" in the "0" and "2"
spot could not exist (aka. "xxx1x1" is an illegal configuration).
The resulting data pool held all possible cliques of the graph and the string
with the largest number of ones would be the maximum clique.
Then, they removed
those cliques that contained illegal connections, because not every node
was interconnected in the original graph (otherwise the entire graph would
be one big clique). The figure on the right shows the illegal paths. For
example, any strand with a "1" in the "0" and "2"
spot could not exist (aka. "xxx1x1" is an illegal configuration).
The resulting data pool held all possible cliques of the graph and the string
with the largest number of ones would be the maximum clique. To create the complete data pool, the scientists utilized DNA pairing
(each nucleic acid has a complement, so if two strands contain a series
of complementary DNA, they will stick to eachother). The scientists arranged
the cliques so each vertex is separated by a string of “connection”
DNA which we’ll call P. Thus, a clique for the six node graph would
be represented as P0V0 P1V1 P2V2 P3V3 P4V4P5V5 P6, where V is each vertex.
The trick is that each Pi of adjacent vertices are complementary strands
of DNA, so scientists need only create strands of DNA for individual nodes
(aka. PoV0 P1, P1V1 P2 etc.) and they will naturally bond together. Thus
the researchers only needed to create two sequences of DNA for each node,
 one to represent the node if it was in the clique (a ‘1’)
and the other to represent if it wasn't in that clique (a ‘0’),
and the complementary ‘P’ strands would bind them together
to form 6 vertex long strands representing all possible cliques. In case
you were curious, the naming standard used was no nucleic acids if the
vertex was a "1" and a predefined sequence of 10 acids if the
vertex was a '0'. Thus it would easy to determine the size of the maximum
clique simply by looking at the lengths of the strands. A method called
“thermal cycling” was used to recursively construct all possible
strands, and the complete/correct strands (those that began with V0 and
ended with V5) were amplified.
one to represent the node if it was in the clique (a ‘1’)
and the other to represent if it wasn't in that clique (a ‘0’),
and the complementary ‘P’ strands would bind them together
to form 6 vertex long strands representing all possible cliques. In case
you were curious, the naming standard used was no nucleic acids if the
vertex was a "1" and a predefined sequence of 10 acids if the
vertex was a '0'. Thus it would easy to determine the size of the maximum
clique simply by looking at the lengths of the strands. A method called
“thermal cycling” was used to recursively construct all possible
strands, and the complete/correct strands (those that began with V0 and
ended with V5) were amplified.
The next step, removing cliques that cannot exist for the graph is a bit more difficult and requires a large amount of manual labor. Although I will not go into the biology, the process involves cutting strands at specific places using enzymes, dividing the data into separate test tubes, and then using sequential restriction operations to eliminate the strands containing the illegal connection; a process which must be repeated for every non-connection in a graph. Thus, even with a faster construction method, this experiment is not scalable. Finding the final answer is easy; gel electrophoresis will reveal to us the shortest DNA strand, which corresponds to the largest clique.
Diagrams taken from Ouyang, et al. “DNA Solution of the Maximal Clique Problem.” Science 1997 278: 446-449.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||||||