Why Genetic Algorithms Work



Although "survival of the fittest" has seemed to have
worked relatively well in the real world, the questions still
remains about how the concept of a genetic algorithm actually
works in a computer. Currently, there is no accepted general theory
explaining how genetic algorithms work.
Schema Theory
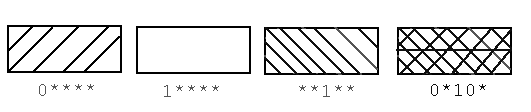
John Holland, the founder of the genetic algorithm field, introduced schema theory to explain how GAs work. Schema describe different bit strings in the search space, and they contain the binary alphabet {0,1,*} where the * is a wildcard that represents either a 0 or 1. The binary representation of the decimal number four is 100, which contains the schemata *00, 1*0, 1**, **0, *0*, and 10*. The defining length of a schema is the distance between the outermost non wildcard symbols. GAs work because thousands of different schema can be processed with relatively few strings. For example, the number four alone represented six different schemata. GAs process many more schema than there are strings in the population. The term implicit parallelism describes the GA's ability to evaluate thousands of different schema patterns simultaneously, or in parallel. Through the process reproduction among the individuals, the "most fit" schemata will increase or decrease their representations in the populations. Holland discovered that a GA effectively processes n3 schemata in a population size of n. The following formula describes the general growth rate of schemata in the search space.
Formula: Consider a function m that describes the number of schema H at a particular time t as m(H,t).
The fittest schemata are more likely to become part of the next
generation while the least fit are less likely. Even though certain
individuals may split during crossover, the schema patterns still
exist. The following animation shows how a schema is preserved
during a crossover.

Building Block Hypothesis
Daniel Goldberg, director of the Illinois Genetic Algorithms Laboratory, proposed that GAs worked because they could find good building blocks. Building blocks are just schemata with a short defining length which consist of bits that work well together. The above animation is an example of a schema with a short defining length that could be a good building block. Goldberg hypothesized that the short, low-order, and highly fit schemata are sampled, recombined, and resampled to form strings of potential higher fitness. However, Goldberg discovered a major weakness of GAs because in order for the building blocks to form, there must be a low epistasis, or interaction, among the genes on a particular chromosome. In other words, if the contribution of a gene to the fitness of a chromosome depends on the value of other genes on the chromosome, then there is high epistatis. For example, bats must be able to produce ultra-sonic squeaks and have specialized hearing in order to detect echoes.

 Principle of Meaningful Building Blocks -- The user should select a coding so that short, low-order schemata are relevant to the underlying problem and relatively unrelated to schemata over other fixed positions.
Principle of Meaningful Building Blocks -- The user should select a coding so that short, low-order schemata are relevant to the underlying problem and relatively unrelated to schemata over other fixed positions. Minimal Alphabets: -- The user should select the smallest alphabet that permits a natural expression of the problem.
Minimal Alphabets: -- The user should select the smallest alphabet that permits a natural expression of the problem.A Graphical View of Schema Theory
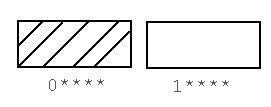
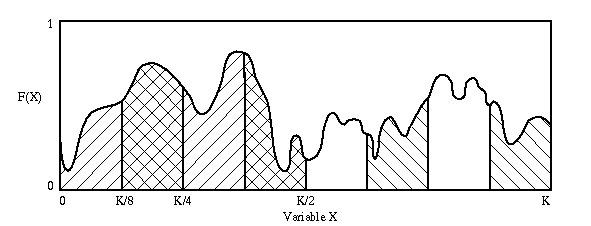
Genetic algorithms are often used to find the global manixum of
a function. The following function F(x) has been partioned into
by two different schema: 0**** and 1****. Since the strings in
the 0**** partition are on average better than the 1**** partition,
the strings with the schema 0**** will become more and more prevalent
in later generations.